Performance of Parallel Programming

PERFORMANCE

Of course our main purpose in writing parallel programs is usually increased performance. So what can we expect? And how can we evaluate our programs?

1. Speedup and efficiency

Usually the best we can hope to do is to equally divide the work among the cores, while at the same time introducing no additional work for the cores. If we succeed in doing this, and we run our program with p cores, one thread or process on each core, then our parallel program will run p times faster than the serial program. If we call the serial run-time T_serial and our parallel run-time T_parallel, then the best we can hope for is T_parallel = T_serial/p. When this happens, we say that our parallel program has linear speedup.

In practice, we’re unlikely to get linear speedup because the use of multiple processes/threads almost invariably introduces some overhead. For example, shared-memory programs will almost always have critical sections, which will require that we use some mutual exclusion mechanism such as a mutex. The calls to the mutex functions are overhead that’s not present in the serial program, and the use of the mutex forces the parallel program to serialize execution of the critical section. Distributed-memory programs will almost always need to transmit data across the network, which is usually much slower than local memory access. Serial programs, on the other hand, won’t have these overheads. Thus, it will be very unusual for us to find that our parallel programs get linear speedup. Furthermore, it’s likely that the overheads will increase as we increase the number of processes or threads, that is, more threads will probably mean more threads need to access a critical section. More processes will probably mean more data needs to be transmitted across the network.

So if we define the speedup of a parallel program to be

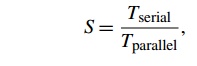
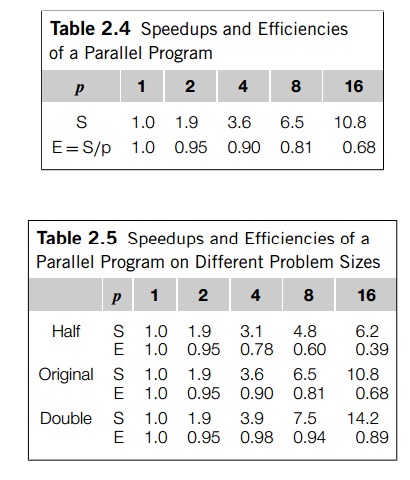
then linear speedup has S = p, which is unusual. Furthermore, as p increases, we expect S to become a smaller and smaller fraction of the ideal, linear speedup p. Another way of saying this is that S=p will probably get smaller and smaller as p increases. Table 2.4 shows an example of the changes in S and S/p as p increases.

This value, S/p, is sometimes called the efficiency of the parallel program. If we substitute the formula for S, we see that the efficiency is

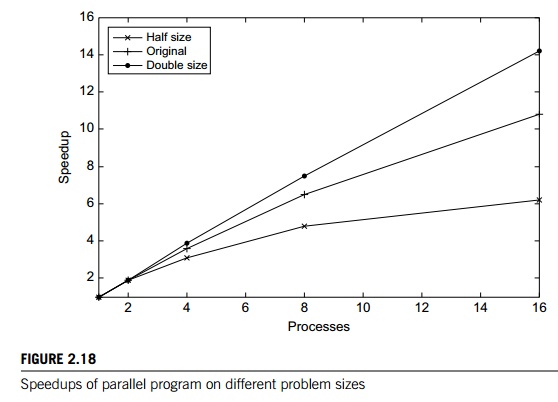
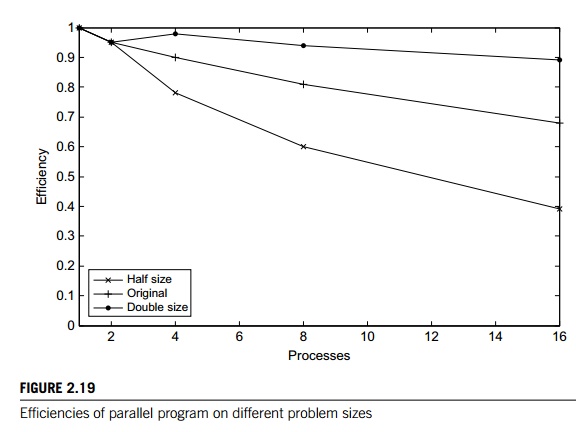
It’s clear that T_parallel, S, and E depend on p, the number of processes or threads. We also need to keep in mind that T_parallel, S, E, and T_serial all depend on the problem size. For example, if we halve and double the problem size of the program whose speedups are shown in Table 2.4, we get the speedups and efficiencies shown in Table 2.5. The speedups are plotted in Figure 2.18, and the efficiencies are plotted in Figure 2.19.

We see that in this example, when we increase the problem size, the speedups and the efficiencies increase, while they decrease when we decrease the problem size. This behavior is quite common. Many parallel programs are developed by dividing the work of the serial program among the processes/threads and adding in the nec-essary “parallel overhead” such as mutual exclusion or communication. Therefore, if T_overhead denotes this parallel overhead, it’s often the case that

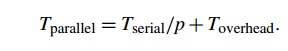
Furthermore, as the problem size is increased, T_overhead often grows more slowly than T_serial. When this is the case the speedup and the efficiency will increase. See Exercise 2.16. This is what your intuition should tell you: there’s more work for the processes/threads to do, so the relative amount of time spent coordinating the work of the processes/threads should be less.

A final issue to consider is what values of T_serial should be used when report-ing speedups and efficiencies. Some authors say that T_serial should be the run-time of the fastest program on the fastest processor available. In practice, most authors use a serial program on which the parallel program was based and run it on a single processor of the parallel system. So if we were studying the performance of a par-allel shell sort program, authors in the first group might use a serial radix sort or quicksort on a single core of the fastest system available, while authors in the second group would use a serial shell sort on a single processor of the parallel system. We’ll generally use the second approach.

2. Amdahl’s law

Back in the 1960s, Gene Amdahl made an observation [2] that’s become known as Amdahl’s law. It says, roughly, that unless virtually all of a serial program is paral-lelized, the possible speedup is going to be very limited—regardless of the number of cores available. Suppose, for example, that we’re able to parallelize 90% of a serial program. Further suppose that the parallelization is “perfect,” that is, regardless of the number of cores p we use, the speedup of this part of the program will be p. If the serial run-time is T_serial= 20 seconds, then the run-time of the parallelized part will be 0.9 xT_serial/p = 18=p and the run-time of the “unparallelized” part will be 0.1 x T_serial = 2. The overall parallel run-time will be

Now as p gets larger and larger, 0.9 T_serial=p = 18=p gets closer and closer to 0, so the total parallel run-time can’t be smaller than 0.1 T_serial = 2. That is, the denom-inator in S can’t be smaller than 0.1 T_serial = 2. The fraction S must therefore be smaller than

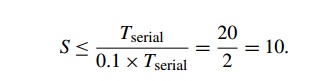
That is, S <= 10. This is saying that even though we’ve done a perfect job in paral-lelizing 90% of the program, and even if we have, say, 1000 cores, we’ll never get a speedup better than 10.

More generally, if a fraction r of our serial program remains unparallelized, then Amdahl’s law says we can’t get a speedup better than 1=r. In our example, r = 1- 0.9 = 1/10, so we couldn’t get a speedup better than 10. Therefore, if a fraction r of our serial program is “inherently serial,” that is, cannot possibly be parallelized, then we can’t possibly get a speedup better than 1=r. Thus, even if r is quite small— say 1/100—and we have a system with thousands of cores, we can’t possibly get a speedup better than 100.

This is pretty daunting. Should we give up and go home? Well, no. There are several reasons not to be too worried by Amdahl’s law. First, it doesn’t take into con-sideration the problem size. For many problems, as we increase the problem size, the “inherently serial” fraction of the program decreases in size; a more mathemat-ical version of this statement is known as Gustafson’s law [25]. Second, there are thousands of programs used by scientists and engineers that routinely obtain huge speedups on large distributed-memory systems. Finally, is a small speedup so awful? In many cases, obtaining a speedup of 5 or 10 is more than adequate, especially if the effort involved in developing the parallel program wasn’t very large.

3. Scalability

The word “scalable” has a wide variety of informal uses. Indeed, we’ve used it several times already. Roughly speaking, a technology is scalable if it can handle ever-increasing problem sizes. However, in discussions of parallel program perfor-mance, scalability has a somewhat more formal definition. Suppose we run a parallel program with a fixed number of processes/threads and a fixed input size, and we obtain an efficiency E. Suppose we now increase the number of processes/threads that are used by the program. If we can find a corresponding rate of increase in the problem size so that the program always has efficiency E, then the program is scalable.

As an example, suppose that T_serial = n, where the units of T_serial are in microsec-onds, and n is also the problem size. Also suppose that T_parallel = n/p + 1. Then

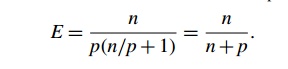
To see if the program is scalable, we increase the number of processes/threads by a factor of k, and we want to find the factor x that we need to increase the problem size by so that E is unchanged. The number of processes/threads will be kp and the problem size will be xn, and we want to solve the following equation for x:

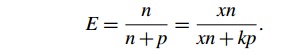
Well, if x = k, there will be a common factor of k in the denominator xn + kp = kn + kp = k(n + p), and we can reduce the fraction to get

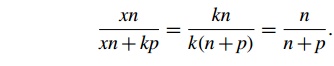
In other words, if we increase the problem size at the same rate that we increase the number of processes/threads, then the efficiency will be unchanged, and our program is scalable.

There are a couple of cases that have special names. If when we increase the number of processes/threads, we can keep the efficiency fixed without increasing the problem size, the program is said to be strongly scalable. If we can keep the efficiency fixed by increasing the problem size at the same rate as we increase the number of processes/threads, then the program is said to be weakly scalable. The program in our example would be weakly scalable.

4. Taking timings

You may have been wondering how we find T_serial and T_parallel. There are a lot of different approaches, and with parallel programs the details may depend on the API. However, there are a few general observations we can make that may make things a little easier.

The first thing to note is that there are at least two different reasons for taking tim-ings. During program development we may take timings in order to determine if the program is behaving as we intend. For example, in a distributed-memory program we might be interested in finding out how much time the processes are spending waiting for messages, because if this value is large, there is almost certainly something wrong either with our design or our implementation. On the other hand, once we’ve com-pleted development of the program, we’re often interested in determining how good its performance is. Perhaps surprisingly, the way we take these two timings is usually different. For the first timing, we usually need very detailed information: How much time did the program spend in this part of the program? How much time did it spend in that part? For the second, we usually report a single value. Right now we’ll talk about the second type of timing. See Exercise 2.22 for a brief discussion of some issues in taking the first type of timing.

Second, we’re usually not interested in the time that elapses between the pro-gram’s start and the program’s finish. We’re usually interested only in some part of the program. For example, if we write a program that implements bubble sort, we’re probably only interested in the time it takes to sort the keys, not the time it takes to read them in and print them out. We probably can’t use something like the Unix shell command time, which reports the time taken to run a program from start to finish.

Third, we’re usually not interested in “CPU time.” This is the time reported by the standard C function clock. It’s the total time the program spends in code executed as part of the program. It would include the time for code we’ve written; it would include the time we spend in library functions such as pow or sin; and it would include the time the operating system spends in functions we call, such as printf and scanf. It would not include time the program was idle, and this could be a prob-lem. For example, in a distributed-memory program, a process that calls a receive function may have to wait for the sending process to execute the matching send, and the operating system might put the receiving process to sleep while it waits. This idle time wouldn’t be counted as CPU time, since no function that’s been called by the process is active. However, it should count in our evaluation of the overall run-time, since it may be a real cost in our program. If each time the program is run, the process has to wait, ignoring the time it spends waiting would give a misleading picture of the actual run-time of the program.

Thus, when you see an article reporting the run-time of a parallel program, the reported time is usually “wall clock” time. That is, the authors of the article report the time that has elapsed between the start and finish of execution of the code that the user is interested in. If the user could see the execution of the program, she would hit the start button on her stopwatch when it begins execution and hit the stop button when it stops execution. Of course, she can’t see her code executing, but she can modify the source code so that it looks something like this:

double start, finish;

. . .

start = Get_current_time();

/*       Code that we want to time      */

. . .

finish = Get_current time();

printf("The elapsed time = %e seconds\n", finish-start);

The function Get_current_time() is a hypothetical function that’s supposed to at’s supposed to return the number of seconds that have elapsed since some fixed time in the past. It’s just a placeholder. The actual function that is used will depend on the API. For example, MPI has a function MPI Wtime that could be used here, and the OpenMP API for shared-memory programming has a function omp get wtime. Both functions return wall clock time instead of CPU time.

There may be an issue with the resolution of the timer function. The resolution is the unit of measurement on the timer. It’s the duration of the shortest event that can have a nonzero time. Some timer functions have resolutions in milliseconds (10 ³ seconds), and when instructions can take times that are less than a nanosecond (10 ⁹ seconds), a program may have to execute millions of instructions before the timer reports a nonzero time. Many APIs provide a function that reports the resolution of the timer. Other APIs specify that a timer must have a given resolution. In either case we, as the programmers, need to check these values.

When we’re timing parallel programs, we need to be a little more careful about how the timings are taken. In our example, the code that we want to time is probably being executed by multiple processes or threads and our original timing will result in the output of p elapsed times.

private double start, finish;

. . .

start = Get_current_time();

/*       Code that we want to time      */

. . .

finish = Get_current_time();

printf("The elapsed time = %e seconds\n", finish-start);

However, what we’re usually interested in is a single time: the time that has elapsed from when the first process/thread began execution of the code to the time the last process/thread finished execution of the code. We often can’t obtain this exactly, since there may not be any correspondence between the clock on one node and the clock on another node. We usually settle for a compromise that looks something like this:

shared double global_elapsed;

private double my_start, my_finish, my_elapsed;

/*       Synchronize all processes/threads     */

Barrier();

my_start = Get_current_time();

/*       Code that we want to time      */

. . .

my_finish = Get_current_time();

my_elapsed = my_finish -  my_start;

/* Find the max across all processes/threads */

 global_elapsed = Global max(my_elapsed);

if (my rank == 0)

printf("The elapsed time = %e seconds\n", global elapsed);

shared double global elapsed;

Here, we first execute a barrier function that approximately synchronizes all of the processes/threads. We would like for all the processes/threads to return from the call simultaneously, but such a function usually can only guarantee that all the process-es/threads have started the call when the first process/thread returns. We then execute the code as before and each process/thread finds the time it took. Then all the process-es/threads call a global maximum function, which returns the largest of the elapsed times, and process/thread 0 prints it out.

We also need to be aware of the variability in timings. When we run a program several times, it’s extremely likely that the elapsed time will be different for each run. This will be true even if each time we run the program we use the same input and the same systems. It might seem that the best way to deal with this would be to report either a mean or a median run-time. However, it’s unlikely that some outside event could actually make our program run faster than its best possible run-time. So instead of reporting the mean or median time, we usually report the minimum time.

Running more than one thread per core can cause dramatic increases in the variability of timings. More importantly, if we run more than one thread per core, the system will have to take extra time to schedule and deschedule cores, and this will add to the overall run-time. Therefore, we rarely run more than one thread per core.

Finally, as a practical matter, since our programs won’t be designed for high-performance I/O, we’ll usually not include I/O in our reported run-times.