Chapter: Optical Communication and Networking : Transmission Characteristics of Optical Fiber
Overall fiber dispersion
Overall fiber dispersion
1. Multimode fibers
The overall dispersion in multimode fibers comprises both chromatic and intermodal terms. The total rms pulse broadening sT is given (see Appendix D) by:

where sc is the intramodal or chromatic broadening and sn is the intermodal broadening caused by delay differences between the modes (i.e. ss for multimode step index fiber and sg for multimode graded index fiber). The chromatic term sc consists of pulse broadening due to both material and waveguide dispersion. However, since waveguide dispersion is generally negligible compared with material dispersion in multimode fibers, thensc =sm.
2. Single-mode fibers
The pulse broadening in single-mode fibers results almost entirely from chromatic or intramodal dispersion as only a single-mode is allowed to propagate.* Hence the bandwidth is limited by the finite spectral width of the source. Unlike the situation in multimode fibers, the mechanisms giving chromatic dispersion in single-mode fibers tend to be interrelated in a complex manner. The transit time or specific group delay sg for a light pulse propagating along a unit length of single-mode fiber may be given as:

where c is the velocity of light in a vacuum, b is the propagation constant for a mode within the fiber core of refractive index n1 and k is the propagation constant for the mode in a vacuum.
The total first-order dispersion parameter or the chromatic dispersion of a single-mode fiber, DT, is given by the derivative of the specific group delay with respect to the vacuum wavelength l as:

In common with the material dispersion parameter it is usually expressed in units of ps nm−1 km−1. When the variable l is replaced by w, then the total dispersion parameter becomes:

The fiber exhibits intramodal dispersion when b varies nonlinearly with wavelength. b may be expressed in terms of the relative refractive index difference D and the normalized propagation constant b as

The rms pulse broadening caused by chromatic dispersion down a fiber of length L is given by the derivative of the group delay with respect to wavelength as [Ref. 45]:
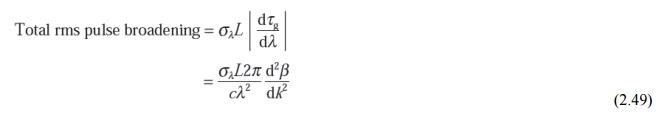
where sl is the source rms spectral linewidth centered at a wavelength l. When Eq. (2.44) is substituted into Eq. (2.45), detailed calculation of the first and second derivatives with respect to k gives the dependence of the pulse broadening on the fiber material’s properties and the normalized propagation constant b. This gives rise to three interrelated effects which involve complicated cross-product terms. However, the final expression may be separated into three composite dispersion components in such a way that one of the effects dominates each terms. The dominating effects are as follows:
ü The material dispersion parameter DM defined by l/c | d2n/dl| where n = n1 or n2 for the core or cladding respectively.
ü The waveguide dispersion parameter DW, which may be obtained from Eq. (3.47) by substitution from Eq. (2.114) for tg, is defined as:

where V is the normalized frequency for the fiber. Since the normalized propagation constant b for a specific fiber is only dependent on V, then the normalized waveguide dispersion coefficient Vd2(Vb)/dV2 also depends on V. This latter function is another universal parameter which plays acentral role in the theory of singlemode fibers.
A profile dispersion parameter DP which is proportional to dD/dl
This situation is different from multimode fibers where the majority of modes propagate far from cutoff and hence most of the power is transmitted in the fiber core. In the multimode case the composite dispersion components may be simplified and separated into two chromatic terms which depend on either material or waveguide dispersion. Also, especially when considering step index multimode fibers, the effect of profile dispersion is negligible. Strictly speaking, in single-mode fiber with a power-law refractive index profile the composite dispersion terms should be employed. Nevertheless, it is useful to consider the total first-order dispersion DT in a practical single-mode fiber as comprising:

Related Topics