Intermodal dispersion

Intermodal dispersion

Pulse broadening due to intermodal dispersion (sometimes referred to simply as modal or mode dispersion) results from the propagation delay differences between modes within a multimode fiber. As the different modes which constitute a pulse in a multimode fiber travel along the channel at different group velocities, the pulse width at the output is dependent upon the transmission times of the slowest and fastest modes. This dispersion mechanism creates the fundamental difference in the overall dispersion for the three types of fiber. Thus multimode step index fibers exhibit a large amount of intermodal dispersion which gives the greatest pulse broadening. However, intermodal dispersion in multimode fibers may be reduced by adoption of an optimum refractive index profile which is provided by the near-parabolic profile of most graded index fibers.

Hence, the overall pulse broadening in multimode graded index fibers is far less than that obtained in multimode step index fibers (typically by a factor of 100). Thus graded index fibers used with a multimode source give a tremendous bandwidth advantage over multimode step index fibers. Under purely single-mode operation there is no intermodal dispersion and therefore pulse broadening is solely due to the intramodal dispersion mechanisms. In theory, this is the case with single-mode step index fibers where only a single mode is allowed to propagate. Hence they exhibit the least pulse broadening and have the greatest possible bandwidths, but in general are only usefully operated with single-mode sources.

In order to obtain a simple comparison for intermodal pulse broadening between multimode step index and multimode graded index fibers, it is useful to consider the geometric optics picture for the two types of fiber.

1. Multimode step index fiber

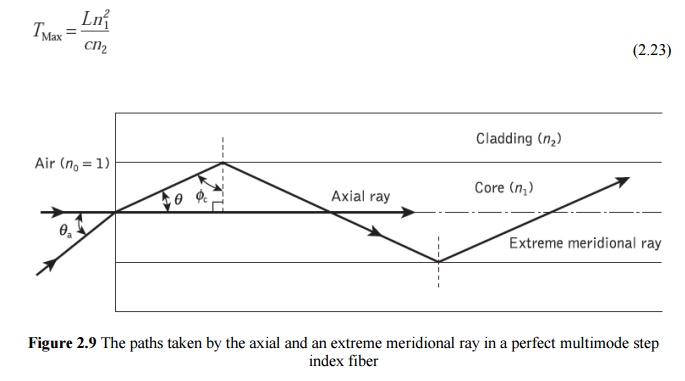
Using the ray theory model, the fastest and slowest modes propagating in the step index fiber may be represented by the axial ray and the extreme meridional ray (which is incident at the core–cladding interface at the critical angle φc) respectively. The paths taken by these two rays in a perfectly structured step index fiber are shown in Figure 2.9. The delay difference between these two rays when traveling in the fiber core allows estimation of the pulse broadening resulting from intermodal dispersion within the fiber. As both rays are traveling at the same velocity within the constant refractive index fiber core, then the delay difference is directly related to their respective path lengths within the fiber. Hence the time taken for the axial ray to travel along a fiber of length L gives the minimum delay time TMin and:

where n1 is the refractive index of the core and c is the velocity of light in a vacuum.

The extreme meridional ray exhibits the maximum delay time TMax where:

Using Snell’s law of refraction at the core–cladding interface following Eq. (2.2):

where n2 is the refractive index of the cladding. Furthermore, substituting into Eq. (2.21) for cosq gives:

The delay difference dTs between the extreme meridional ray and the axial ray may be obtained by:

where D is the relative refractive index difference. However, when D<< 1, then from the definition given by Eq. (2.9), the relative refractive index difference may also be given approximately by:

where NA is the numerical aperture for the fiber. The approximate expressions for the delay difference given in Eqs (2.27) and (2.28) are usually employed to estimate the maximum pulse broadening in time due to intermodal dispersion in multimode step index fibers. Again considering the perfect step index fiber, another useful quantity with regard to intermodal dispersion on an optical fiber link is the rms pulse broadening resulting from this dispersion mechanism along the fiber. When the optical input to the fiber is a pulse pi(t) of unit area, as illustrated in Figure 2.10, then

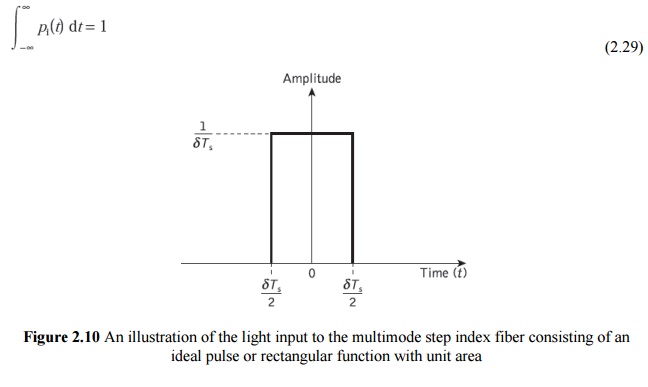
It may be noted that pi(t) has a constant amplitude of 1/dTs over the range:

The rms pulse broadening at the fiber output due to intermodal dispersion for the multimode step index fiber ss (i.e. the standard deviation) may be given in terms of the variance ss2:

Where M1 is the first temporal moment which is equivalent to the mean value of the pulse and M2, the second temporal moment, is equivalent to the mean square value of the pulse.

Hence:

The mean value M1 for the unit input pulse of Figure 2.10 is zero, and assuming this is maintained for the output pulse, then from Eqs (2.30) and (2.32):

Integrating over the limits of the input pulse (Figure 3.12) and substituting for pi(t) in Eq. (2.33) over this range gives:

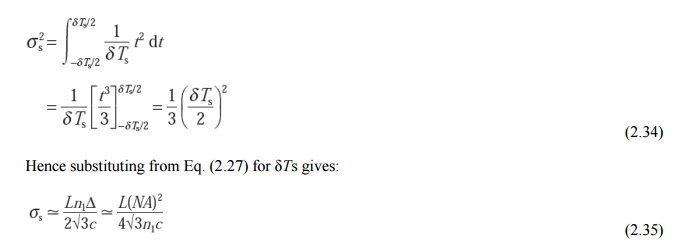
Equation (2.35) allows estimation of the rms impulse response of a multimode step index fiber if it is assumed that intermodal dispersion dominates and there is a uniform distribution of light rays over the range 0≤q≤qa The pulse broadening is directly proportional to the relative refractive index difference D and the length of the fiber L. The latter emphasizes the bandwidth–length trade-off that exists, especially with multimode step index fibers, and which inhibits their use for wideband long-haul (between repeaters) systems. Furthermore, the pulse broadening is reduced by reduction of the relative refractive index difference D for the fiber.

Intermodal dispersion may be reduced by propagation mechanisms within practical fibers. For instance, there is differential attenuation of the various modes in a step index fiber. This is due to the greater field penetration of the higher order modes into the cladding of the waveguide. These slower modes therefore exhibit larger losses at any core–cladding irregularities, which tends to concentrate the transmitted optical power into the faster lower order modes. Thus the differential attenuation of modes reduces intermodal pulse broadening on a multimode optical link.

Another mechanism which reduces intermodal pulse broadening in nonperfect (i.e. practical) multimode fibers is the mode coupling or mixing. The coupling between guided modes transfers optical power from the slower to the faster modes, and vice versa. Hence, with strong coupling the optical power tends to be transmitted at an average speed, which is the mean of the various propagating modes. This reduces the intermodal dispersion on the link and makes it advantageous to encourage mode coupling within multimode fibers.

The expression for delay difference given in Eq. (2.27) for a perfect step index fiber may be modified for the fiber with mode coupling among all guided modes to:

2. Multimode graded index fiber

Intermodal dispersion in multimode fibers is minimized with the use of graded index fibers. Hence, multimode graded index fibers show substantial bandwidth improvement over multimode step index fibers. The reason for the improved performance of graded index fibers may be observed by considering the ray diagram for a graded index fiber shown in Figure 2.11. The fiber shown has a parabolic index profile with a maximum at the core axis, as illustrated in Figure 2.11(a). Analytically, the index profile is given by:

Figure 2.11(b) shows several meridional ray paths within the fiber core. It may be observed that apart from the axial ray, the meridional rays follow sinusoidal trajectories of different path lengths which result from the index grading. However, the local group velocity is inversely proportional to the local refractive index and therefore the longer sinusoidal paths are compensated for by higher speeds in the lower index medium away from the axis.

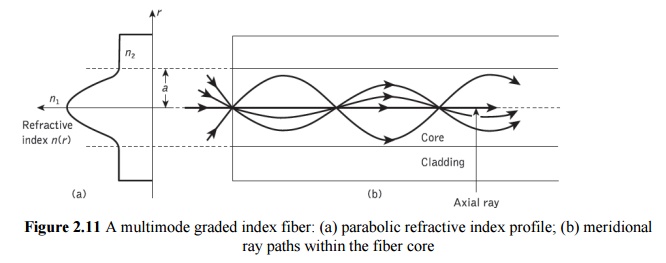
Hence there is an equalization of the transmission times of the various trajectories towards the transmission time of the axial ray which travels exclusively in the high-index region at the core axis, and at the slowest speed. As these various ray paths may be considered to represent the different modes propagating in the fiber, then the graded profile reduces the disparity in the mode transit times.

The dramatic improvement in multimode fiber bandwidth achieved with a parabolic or near-parabolic refractive index profile is highlighted by consideration of the reduced delay difference between the fastest and slowest modes for this graded index fiber dTg. Using a ray theory approach the delay difference is given by:

However, a more rigorous analysis using electromagnetic mode theory gives an absolute temporal width at the fiber output of :

which corresponds to an increase in transmission time for the slowest mode of D2/8 over the fastest mode. The expression given in Eq. (2.39) does not restrict the bandwidth to pulses with time slots corresponding to dTg as 70% of the optical power is concentrated in the first half of the interval. Hence the rms pulse broadening is a useful parameter for assessment of intermodal dispersion in multimode graded index fibers. It may be shown that the rms pulse broadening of a near-parabolic

index profile graded index fiber sg is reduced compared with similar broadening for the corresponding step index fiber ss (i.e. with the same relative refractive index difference) following

where D is a constant between 4 and 10 depending on the precise evaluation and the exact optimum profile chosen.

The best minimum theoretical intermodal rms pulse broadening for a graded index fiber with an optimum characteristic refractive index profile for the core aop of