Number System Conversions

Number System Conversions

1. Decimal to Binary Conversion

2. Decimal to Octal Conversion

3. Decimal to Hexadecimal Conversion

4. Conversion of fractional Decimal to Binary

5. Binary to Decimal Conversion

6. Binary to Octal Conversion

7. Binary to Hexadecimal Conversion

8. Conversion of fractional Binary to Decimal equivalent

9. Octal to Decimal Conversion

10. Octal to Binary Conversion

11. Hexadecimal to Decimal Conversion

1. Decimal to Binary Conversion

Generally two methods followed.

Method 1: To convert Decimal to Binary “Repeated Division by 2” method can be used. Any Decimal number divided by 2 will leave a remainder of 0 or 1. Repeated division by 2 will leave a sequence of 0s and 1s that become the binary equivalent of the decimal number. Suppose it is required to convert the decimal number N into binary form, dividing N by 2 in the decimal system, we will obtain a quotient N1 and a remainder R1, where R1 can have a value of either 0 or 1. The process is repeated until the quotient becomes 0 or 1. When the quotient is ‘0’ or ‘1’, it is the final remainder value. Write the final answer starting from final remainder value obtained to the first remainder value obtained.

Example

Convert (65)₁₀ into its equivalent binary number

Method 2 : Sum of Powers of 2.

A decimal number can be converted into a binary number by adding up the powers of 2 and then adding bits as needed to obtain the total value of the number.

a) Find the largest power of 2 that is smaller than or equal to 65.

65₁₀ > 64₁₀

b) Set the 64’s bit to 1 and subtract 64 from the original number

65-64=1

c) 32 is greater than the remaining total. Therefore, set the 32’s bit to 0.

d) 16 is greater than the remaining total. Therefore, set the 16’s bit to 0.

e) 8 is greater than the remaining total. Therefore, set the 8’s bit to 0.

f) 4 is greater than the remaining total. Therefore, set the 4’s bit to 0.

g) 2 is greater than the remaining total. Therefore, set the 2’s bit to 0.

h) As the remaining value is equivalent to 1’s bit, set it to 1.

1-1=0

Conversion is complete 65₁₀ = (1000001)₂

Example

The conversion steps can be given as follows:

Given Number : 65

Equivalent or value less than power of 2 is : 64

(1) 65 - 64 = 1

(2) 1 - 1= 0

2. Decimal to Octal Conversion

To convert Decimal to Octal, “Repeated Division by 8” method can be used. The method is the same we have learnt in 2.4.1, but in this method, we have to divide the given number by 8.

Example

Convert (65)₁₀ into its equivalent Octal number

3. Decimal to Hexadecimal Conversion

To convert Decimal to Hexadecimal, “Repeated division by 16” method can be used. The method is the same as we have learnt in 2.4.1, but in this method, we have to divide the given number by 16.

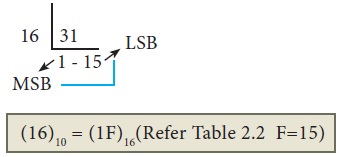
Example

Convert (31)₁₀ into its equivalent hexadecimal number.

4. Conversion of fractional Decimal to Binary

The method of repeated multiplication by 2 has to be used to convert such kind of decimal fractions.

The steps involved in the method of repeated multiplication by 2:

Step 1: Multiply the decimal fraction by 2 and note the integer part. The integer part is either 0 or 1.

Step 2: Discard the integer part of the previous product. Multiply the fractional part of the previous product by 2. Repeat Step 1 until the same fraction repeats or terminates (0).

Step 3: The resulting integer part forms a sequence of 0s and 1s that become the binary equivalent of decimal fraction.

Step 4: The final answer is to be written from first integer part obtained till the last integer part obtained.

Note: Fraction repeats, the product is the same as in the first step.

Write the intger parts from top to bottom to obtain the equivalent fractional binary number. Hence (0.2)₁₀=(0.00110011…)₂ = (0.00110011)₂

5. Binary to Decimal Conversion

To convert Binary to Decimal we can use positional notation method.

Step 1: Write down the Binary digits and list the powers of 2 from right to left(Positional Notation)

Step 2: For each positional notation written for the digit, now write the equivalent weight.

Step 3: Multiply each digit with its corresponding weight

Step 4: Add all the values.

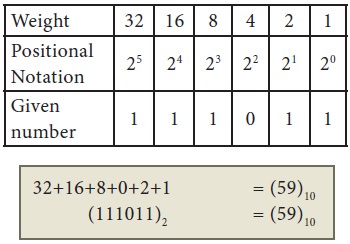
Example

Convert (111011)₂ into its equivalent decimal number.

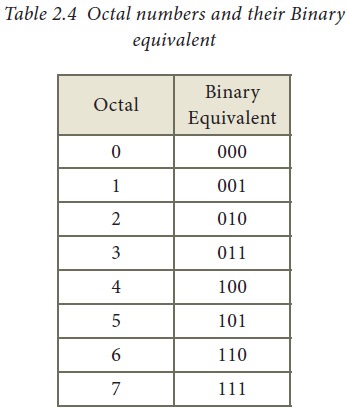
6. Binary to Octal Conversion

Step 1: Group the given binary number into 3 bits from right to left.

Step 2: You can add preceding 0 to make a group of 3 bits if the left most group has less than 3 bits.

Step 3: Convert equivalent octal value using "2's power positional weight method"

Example

Convert (11010110)₂ into octal equivalent number

Step 1: Group the given number into 3 bits from right to left.

011 010 110

Note: The left most groups have less than 3 bits, so 0 is added to its left to make a group of 3 bits.

Step-2: Find Octal equivalent of each group

7. Binary to Hexadecimal Conversion

Step 1: Group the given number into 4 bits from right to left.

Step 2: You can add preceding 0’s to make a group of 4 bits if the left most group has less than 4 bits.

Step 3: Convert equivalent Hexadecimal value using "2's power positional weight method"

Example

Convert (1111010110)₂ into Hexadecimal number

Step 1: Group the given number into 4 bits from right to left.

0011 1101 0110

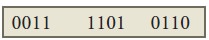
Note: 0’s are added to the left most group to make it a group of 4 bits

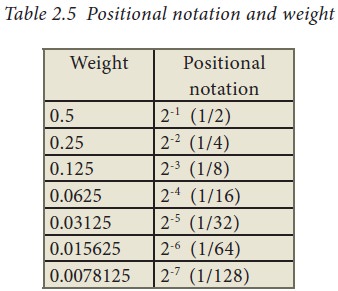
8. Conversion of fractional Binary to Decimal equivalent

Follow the steps to convert fractional Binary number to its Decimal equivalent.

Step 1: Convert integral part of Binary to Decimal equivalent using positional notation method (Procedure is same as discussed in 2.4.5)

Step 2: To convert the fractional part of binary to its decimal equivalent.

Step 2.1: Write down the Binary digits in the fractional part

Step 2.2: For all the digits write powers of 2 from left to right starting from 2^-1, 2^-2, 2^-3...... 2^-n, now write the equivalent weight.

Step 2.3: Multiply each digit with its corresponding weight

Step 2.4: Add all the values which you obtained in Step 2.3

Step 3: To get final answer write the integral part (after conversion), followed by a decimal point(.) and the answer arrived at Step 2.4

Example

Convert the given Binary number (11.011)₂ into its decimal equivalent Integer part (11)₂ = 3 (Refer table 2.2)

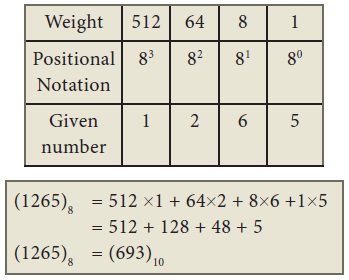
9. Octal to Decimal Conversion

To convert Octal to Decimal, we can use positional notation method.

1.     Write down the Octal digits and list the powers of 8 from right to left(Positional Notation)

2.     For each positional notation of the digit write the equivalent weight.

3.     Multiply each digit with its corresponding weight

4.     Add all the values

Example

Convert (1265)₈ to equivalent Decimal number

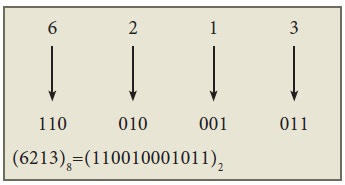
10. Octal to Binary Conversion

For each Octal digit in the given number write its 3 digits binary equivalent using positional notation.

Example

Convert (6213)₈ to equivalent Binary number

 11. Hexadecimal to Decimal Conversion

To convert Hexadecimal to Decimal we can use positional notation method.

 1.    Write down the Hexadecimal digits and list the powers of 16 from right to left(Positional Notation)

2.    For each positional notation written for the digit, now write the equivalent weight.

3.    Multiply each digit with its corresponding weight

4.    Add all the values to get one final value.

Example

Convert (25F)₁₆ into its equivalent Decimal number.

12. Hexadecimal to Binary Conversion

Write 4 bits Binary equivalent for each Hexadecimal digit for the given number using positional notation method.

Example

Convert (8BC)₁₆ into equivalent Binary number