Binary Representation for Signed Numbers

Binary Representation for Signed Numbers

Computers can handle both positive (unsigned) and negative (signed) numbers. The simplest method to represent negative binary numbers is called Signed Magnitude. In signed magnitude method, the left most bit is Most Significant Bit (MSB), is called sign bit or parity bit.

The numbers are represented in computers in different ways:

·     Signed Magnitude representation

·     1’s Complement

·     2’s Complement

1. Signed Magnitude representation

The value of the whole numbers can be determined by the sign used before it. If the number has ‘+’ sign or no sign it will be considered as positive. If the number has ‘–’ sign it will be considered as negative.

Example:

+43 or 43 is a positive number

–43 is a negative number

In signed binary representation, the left most bit is considered as sign bit.

If this bit is 0, it is a positive number and if it 1, it is a negative number. Therefore a signed binary number has 8 bits, only 7 bits used for storing values (magnitude) and the 1 bit is used for sign.

+43 is represented in memory as follows:

-43 can be represented in memory as follows.

2. 1’s Complement representation

This is an easier approach to represent signed numbers. This is for negative numbers only i.e. the number whose MSB is 1.

The steps to be followed to find 1’s complement of a number:

Step 1: Convert given Decimal number into Binary

Step 2: Check if the binary number contains 8 bits , if less add 0 at the left most bit, to make it as 8 bits.

Step 3: Invert all bits (i.e. Change 1 as 0 and 0 as 1)

Example

Find 1’s complement for (–24)₁₀

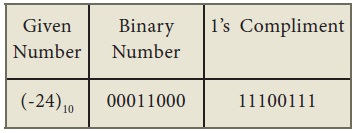
3. 2’s Complement representation

The 2’s-complement method for negative number is as follows:

1.           Invert all the bits in the binary sequence (i.e., change every 0 to1 and every 1 to 0 ie.,1’s complement)

2.           Add 1 to the result to the Least Significant Bit (LSB).

Example

2’s Complement represent of (-24)₁₀

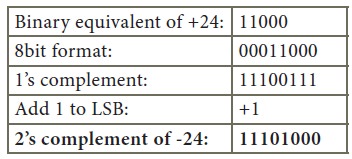
Write the 1’s complement number and 2’s complement number for the following decimal numbers: 

(A) 22  (B) -13  (C) -65 (D) -46