Nuclear Magnetic Resonance Spectroscopy

NUCLEAR MAGNETIC RESONANCE SPECTROSCOPY

INTRODUCTION

Nuclear Magnetic Resonance (NMR) spectroscopy just like IR and UV is regarded as a process whereby energy from an external source is absorbed and brings about a change or resonance to an ‘excited’ or high energy state. The energy required for NMR lies in the low energy or long wavelength radio-frequency end of the electromagnetic spectrum.

Consequent to the magnetic properties of nuclei arising from the axial spin, the emerging radio-frequency gets absorbed in a magnetic field. Therefore, for a particular nucleus an NMR absorption spectrum invariably comprises one to several groups of absorption lines in the ratio-frequency portion of the electromagnetic spectrum. Evidently, the location of peaks indicate the chemical nature of the nucleus, whereas the multiplets provide information regarding the spatial positions of the neighbouring nuclei. Hence, NMR is also known as Nuclear Spin Resonance (NSR) spectroscopy.

NMR has accomplished a growth in a geometrical progression since the early sixties and virtually developed into extremely potential analytical tools not only useful for elucidation of complex structural determinations but also equally beneficial in the assay of pharmaceutical substances.

In reality, NMR spectroscopy has broadened the scope and absolute possibility for performing more extensive as well as intensive studies with regard to recording the spectrum of isolated and synthesized organic molecules in addition to their mechanistic and stereochemical details hitherto inaccessible. There-fore, NMR spectroscopy finds its applications for compound identification, by means of a ‘fingerprint technique’ very much identical to that used in IR-spectroscopy. Besides, it is invariably utilized as a specific method of assay for the individual constituents of a mixture.

1. THE NMR PHENOMENON

Following are the five different aspects that essentially govern the NMR phenomenon, namely :

A. The Spinning Nucleus : 

The nucleus of the hydrogen atom, i.e., the proton, just behaves as if it is a small spinning bar magnet. It does so because it evidently possesses an electrical charge as well as a mechanical spin. Consequently, a spinning charged body will generate a magnetic field, and hence the nu-cleus of hydrogen atom is not an exception.

B. The effect of an External Magnetic Field : 

As a ‘compass needle’ possesses an inherent ten-dency to align itself with the earth’s magnetic field, the proton not only responds to the influence of an external magnetic field but also tends to align itself with that field. However, because of restrictions as applicable to nuclei (not to compass needles) the proton can only adopt the following two orientations with regard to an external magnetic field. At this juncture two situations normally arise, namely :

(a) when proton is aligned with the field (i.e., at lower energy state), and

(b) when proton is opposed to the field (i.e., at higher energy state).

Some NMR-analysts describe these proton orientations as ‘parallel’ with or ‘antiparallel’ with the applied field.

C. The Precessional Motion : 

The proton appears to be behaving as ‘spinning magnet’ and there-fore, not only can it align itself with or oppose an external field, but also may move in a characteristic manner under the influence of the external magnet.

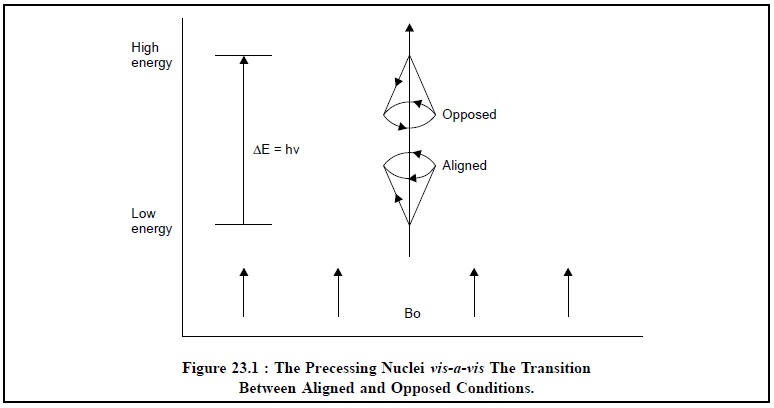
Figure 23.1, represents the precessing nuclei vis-a-vis the transition energy (∆E) of reorientation of magnetic dipole between the aligned and opposed conditions when subjected to an external magnetic field (Bo). It is absolutely clear from this Figure that the proton gets aligned with the external magnetic field only at a lower energy states, while it becomes opposed to the field at higher energy states.

However, the energy of the reorientation of magnetic dipole, ∆E, may be expressed as follows :

∆E = hν

where, h = Planck’s constant, and

v= Frequency of radiation.

In order to understand the precessional motion more vividly, let us take the example of a spinning ‘top’ and its spinning motion. The top will (unless absolutely vertical) also perform a comparatively slower waltz-like motion whereby the spinning axis of the top moves slowly around the vertical. This particular phenomenon is known as the precessional motion and hence, the ‘top’ is generally said to be precessing around the vertical axis of the earth’s gravitational field. In other words, the precession comes into effect due to the interaction of spin (i.e., gyroscopic motion) with the earth’s gravity vertically downwards. Therefore, a spinning top will precess, whereas a static top will fall over (not precess).

D. The Precessional Frequency : 

The spinning frequency of the nucleus does not change at all, whereas the speed of precession does. Therefore, ν ∝ Bo, i.e., the precessional frequency is directly propor-tional to the strength of the external field Bo.

It designates one of the most important relationships in NMR-spectroscopy.

Example : A proton expressed to an external magnetic force of 1.4 T (≡ 14, 000 gauss) will precess ~ 60 million times per second so that the precessional frequency ν = 60 MHz ; and for an external field of 2.3 T, ν ≈ 100 MHz, and at 5.1 T, ν ≈ 200 MHz.

E. The Energy Transitions : 

Whenever a proton is precessing in the aligned orientation (low energy) it can absorb energy and pass into the orientation (high energy) ; and subsequently it can lose this extra energy and relax back into the aligned state.

Interestingly, the precessing proton can only absorb energy from the radio frequency source if the precessing frequency is exactly the same as that of the radio frequency beam ; and when this particular situation arises, the nucleus and the radio frequency beam are said to be in resonance, thereby justifying the term ‘nuclear magnetic resonance’.

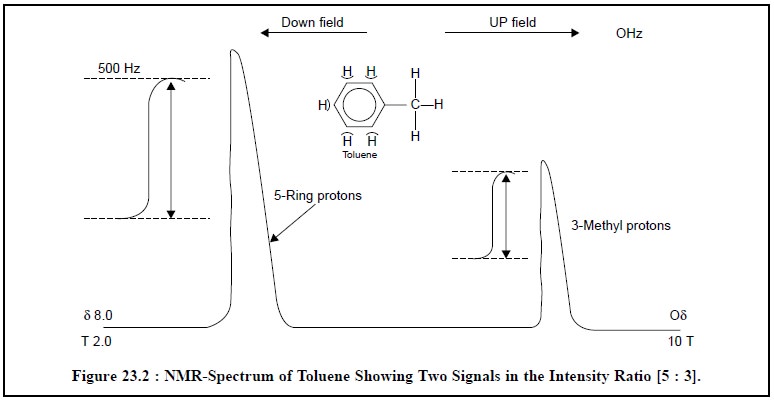
In NMR spectroscopy, the precessing protons of an organic molecule, after being duly exposed to a powerful external magnetic field (ranging between 60-400 MHz), are irradiated with radio frequency energy of the appropriate frequencies, thereby promoting protons from the low-energy (aligned state) to the high-energy (opposed state). The absorption of energy is ultimately recorded in the form of NMR spectrum as shown in Figure 23.2.

2. INFORMATIONS PROVIDED BY  ¹H-NMR (PROTON-NMR)

¹H-NMR provides a number of valuable informations stated below, which are employed for the struc-tural elucidation as well as assay of important pharmaceutical substances, namely :

(i) To record differences in the magnetic properties of the various nuclei present,

(ii) To deduce in large measure the exact locations of these nuclei within the molecule,

(iii) To deduce how many different types of hydrogen environments are present in the molecule,

(iv) To deduce which hydrogen atoms are present on neighbouring carbon atoms, and

(v) To measure exactly how many H-atoms are actually present in each of these environments.

Example : Figure 23.2 depicts the NMR-spectrum of toluene (C₆H₅—CH₃), which essentially pos-sesses two different species of H-atoms, for instance :

(a) methyl hydrogen atoms (—CH₃), and

(b) aromatic ring hydrogen atoms (—C₆H₅).

Hence, two signals will show-up in the NMR-spectrum corresponding to these two different chemical and magnetic environments. Furthermore, the areas under each signal are in the ratio of the number of protons in each part of the molecule, and thus actual measurement will reveal that the ratio of these areas is 5 : 3.