Nuclear Magnetic Resonance Spectroscopy: Theory

THEORY

Almost fifty per cent of the nuclei known so far behave as if they were spinning as a whole about an axis just like a minute bar magnet, the axis of which happens to be coincident with the axis of spin. The angular momentum of the charge created by the spinning electrons may be expressed in terms of spin quan-tum number designated as ‘I’ (in units of h/2π were h is Planck’s constant). Therefore, for a nuclei to exhibit NMR phenomenon the spin quantum number I is always greater than 0. The spin quantum number I is directly associated with the mass number and the atomic number of the nuclei. Pope et al. (1959) has put forward a detailed list of spin quantum values vis-a-vis mass number and atomic number so as to facilitate in establishing the value of I empirically as shown below :

From the above useful data provided one may draw an inference that spin numbers have either ‘inte gral’ or ‘half-integral’ values ranging from 1/2 to at least 9/2 for different nuclei. The spin number is obtained by the addition of individual protons and neutron spin numbers of ½ each, with the restriction that neutrons can cancel only neutrons and protons can cancel only protons.

Precisely three classes of nuclei may be neatly distinguished, namely :

(a) Zero-spin (I = O) : Those where both the number of protons and neutrons are even, for instance : ¹²C, ¹⁶O, and ³²S. Nuclei in this category do not interfere with a NMR-signal from other nuclei. In case, ¹²C and ¹⁶O has also been magnetic per chance, the NMR spectra of organic molecules cer-tainly would have been much more difficult and complex.

(b) Half-Integral Spin: Those where either the number of protons or the number of neu trons is odd. This constitutes the most important group of nuclei for their immense applications and utility to a medicinal chemist and an organic chemist.

Examples* : They are ¹H ; ³H ;¹³C ^{; 19}F ^{; 31}P ; ¹⁵N ; ²⁹S ;

(c) Integral Spin (I = 1/2) : Those where both the number of protons and the number of neutrons is odd.

Examples : Where 1 = 1, are : ²H (Deuterium) and ¹⁴N ; and where I > 1 are : ¹⁰B ; ¹¹B ; ³⁵Cl ; ¹⁷O ; ²⁷Al ;

In other words, isotopes having a spin value equal to, or greater than one exhibit an ellipsoidal charge distribution and have spin. They invariably possess a nuclear electric quadrupole moment, desig-nated as ‘Q’.

1. ORIENTATIONS OF MAGNETIC NUCLEUS UNDER Bo

Under the influence of external magnetic field, Bo, a magnetic nucleus may take up different orientations with regard to that field, for instance :

(i) Two orientations : The number of possible orientation is given by (2I + 1), so that for nuclei with spin    ¹ e.g., ¹H, ¹³C, ¹⁹F only two orientations are allowed, and 2

(i)          Three orientations : Both ²H (Deuterium) and ¹⁴N have I = 1 and, therefore, can take up three orientations. These nuclei essentially possess both electric quadrupoles and magnetic dipoles.

2.  PRECESSIONAL FREQUENCY (ν)

In any magnetic field, magnetic nuclei like the proton precess at a frequency ν, which is proportional to the strength of the applied field. The exact frequency is expressed by :

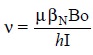
where, Bo = Strength of the external field experienced by the proton,

I = Spin quantum number,

h = Planck’s constant (6.626 × 10 ^–34 Js),

μ= Magnetic moment of the particular nucleus, and

β_N = Nuclear magnet on constant.

Table 23.1 records some typical approximate values of ‘ν’ for (a) selected values of field strength Bo, and (b) common magnetic nuclei.

(Free Electron) 3.9 × 10 ⁴

The data from Table 23.1, reveals that :

(a) magnetic moments of ¹H and ¹⁹F are relatively large and, therefore, detection NMR-signals with these nuclei are fairly sensitive,

(b) Magnetic moment of ¹³C is almost 1/4 that of ¹H i.e., the former is less sensitively detected in NMR as compared to the latter,

(c) Similarly, magnetic moment of ²H (Deuterium) is approximately 1/6th that of ¹H (less sensitively detected in NMR), and

(d) Even with very large magnetic fields, upto 7.1 T, the energy difference (∆ = hν) is very small, upto 300 MHz ; because the difference is so small ( ₋~ 10^–4 kJ mol^–1) the number of protons in the two energy states are almost equal.

3. SATURATION OF THE SIGNAL

It has been observed that nuclei in the lower energy state undergo transitions to the higher energy state. The populations of the two states may approach equality, and if this situation arises no further net absorption of energy take place, and the observed NMR resonance signal will fade out. This particular situation is termed as saturation of the signal.

It is pertinent to mention here that in a small NMR spectrum the populations in the two spin states never become equal, by virtue of the fact that higher energy nuclei are constantly returning to the lower energy spin state.

4. ABSORPTION POSITIONS IN NMR-SPECTRUM

For different types of organic compounds and pharmaceutical substances the resonance positions for protons lie usually within a narrow range (~ 600 Hz). As the differences in the signal’s positions are small in comparison to the applied frequency (60 × 10 ⁶ Hz or 60 MHz), therefore, the absolute measurements of absorption positions cannot be made with the required degree of accuracy (0.1 Hz 60 × 10 ⁶ Hz, i.e., 1 part in 10⁸). However, it is quite possible to measure the differences in frequency relative to a standard substance with the required degree of accuracy and precision.

5. CHEMICAL SHIFT

The chemical shift (δ) is defined as the difference between the resonance position of a nucleus and that of a standard reference compound. It is normally expressed in terms independent of Ho (or the related applied resonance frequency ν) :

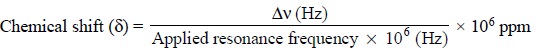
where, ∆ν = Difference in frequency (Hz) between the observed signal and that of the standard (reference compound).

Reference Compound : For ¹H NMR i.e., Proton-NMR, tetramethyl silane (TMS), (CH₃)₄Si, is employed mostly as the reference compound, because of the fact that its protons resonate at higher field strength than most other protons.

Convention for δ : TMS assigned (δ = 0), values for other protons are measured positively downfield.

In other words, increasing δ corresponds to increasing de-shielding of the nucleus.

6.  SPIN-SPIN INTERACTIONS

High resolution NMR spectra very often exhibit signals as multiplets, invariably showing a more or less symmetrical appearance.

Multiplicity is brought about due to the splitting of the signal of one set of equivalent nuclei by the magnetic fields of adjacent sets of nuclei i.e., spin-spin interactions. The distance between the peaks of a regular multiplet is termed as the coupling constant, designated as J, and measured in Hz.

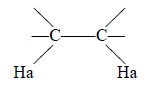
The protons Ha and Hb are totally in different chemical environments. There is a significant differ-ence in their chemical shifts because of the variance in the resonance positions of their nuclei. Thus, Ha experiences a total magnetic field comprising of : external field (Ho) and local field due to Hb as shown in Figure 23.3.

From Figure 23.3, it is evident that Ha, at a given constant, experiences the local field of Hb that may be either aligned with or against that of Ha.

The Ha signal is split into a doublet and the peaks of this doublet will be equal in height, because each alignment of spins has equal probability.

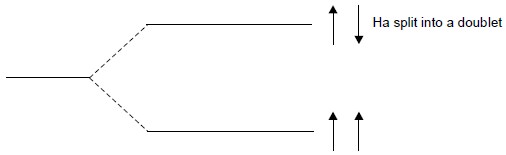
Based on the same reasonings, the signal emerged from Hb is split into a doublet as shown below : The spin-alignments of Hb₁ and Hb₂ may be designated as :

The probability of each of the above cited four spin arrangements is equal, two having the same energy ; thereby giving rise to a triplet for the signal of Ha, having peak heights in the ratio 1 : 2 : 1.

Therefore, generalizing the spin-spin interactions cause a signal to be split into (n + 1) peaks, where ‘n’ is the number of interacting nuclei on the adjacent carbon atom.

Hence, two important observations are usually made, namely :

(a) Coupling constant, J, is independent of Ho (contrast with δ), and

(b) Regular multiplets are produced when the difference in chemical shifts (in Hz) between nuclei A and X (i.e., ∆ν_AX) is large relative to the coupling constant J_AX, i.e., when ∆νA_X/JAX ≥ ∼ 10.

The spectra obtained in this manner designated as First Order, and these may be analysed with the help of the following FOUR general RULES, namely :

RULE : 1 : Multiplets caused by mutual interaction of nuclei A and nuclei X have identical J values,

RULE : 2 : Interaction of nucleus A with a group of n magnetically equivalent nuclei X (of spin IX), produces a multiplet of (2n_x, Ix + 1) peaks,

RULE : 3 : Intensities of the multiplet are asymmetrical about the mid-point of the signal, that corre-sponds to the origin of the multiplet and is equal to the chemical shift.

Pascal’s Triangle : The nuclei having spin quantum number I = 1/2, relative intensities of the multiplet’s peak are given by the coefficients of the binomial expansion, (1 + x)ⁿ, where n = number of nuclei interacting with the specific nucleus emitting the signal ; or by Pascal’s Triangle as given below :

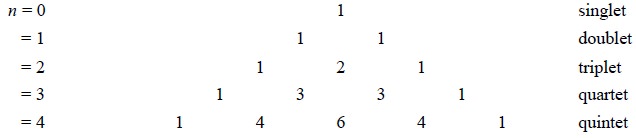
RULE : 4 : Interaction is normally observable between close groups of magnetically non-equivalent nuclei.

This exclusively deals with nuclei of spin 1/2 and, therefore, the examples and applications shall be given from ¹H i.e., proton magnetic resonance (PMR) spectroscopy.

However, a brief description of the following three types of NMR-spectroscopy will be made here so as to apprise the readers about their principles and main usages only, such as :

(i) ³H-NMR (Tritium NMR Spectrocopy),

(ii) ¹³C-NMR Spectroscopy, and

(iii) 2D-NMR (Two Dimensional Correlation Spectrocopy ; or Two Dimensional COSY Spectrum).

7. ³H-NMR (TRITIUM NMR-SPECTROSCOPY)

The ease with which ‘tritium’ could be employed for labelling organic compounds, having fairly high molar specific activity, has turned it into a very useful and versatile β-emitting radionuclide for chemi-cal and life sciences research. The unique novel characteristic feature of tritium tracers being that it may be used as a tracer for carbon as well as hydrogen structures. A non-destructive method of analysis was initiated in Great Britain* employed elaborated sophistically designed instrumentations** armed with ‘supercon’ magnets and latest computer technology.

The comprehensive dedicated research ultimately made it possible to decode the patterns of labelling in almost any type of tritium labelled compound at low isotopic abundance (e.g., 3 × 10 ^–4 to 3 × 10 ^–2 per cent. ³H per site) with the aid of ³H-NMR directly, rapidly, reliably and non-destructive analytical means. Since, 1971, the ³H-NMR spectroscopy, utilizing only millicurie (mCi) quantities of radioactivity, emerged as a most useful analytical tool for the study of tritium labelled compounds.

The two major advantages of ³H-NMR spectroscopy based on the characteristic magnetic features of the tritium nucleus are, namely :

(a) High receptivity of the tritium nucleus, i.e., only small amounts of radioactivity (0.1 to 10 mCi per site, 3.7 to 370 MBq) are needed to bring about a well-defined spectrum, and

(b) Similarity of the chemical shifts of ³H nuclei and those of ¹H nuclei (protons) i.e., the copious volume of available data on ‘proton-chemical shifts’ may be applied directly for the interpretation of ³H-NMR spectra. In other words no new correlations need to be determined, as in the case for ¹³C-NMR-sepctroscopy.

The various advantages of ³H-NMR spectroscopy are, namely :

·              a rapid direct and non-destructive method,

·              provides direct information on regiospecificity,

·              gives quantitative distribution of the label,

·              caters for accurate and precise information on the stereochemistry of the label, and

·              requires only millicuries (mCi) rather than microcuries or lesser amounts of radioactivity.

Table 23.2, records the nuclear properties of ¹H, ³H (T) and ¹³C isotopes being employed particularly in various arms of ‘Life Sciences’ :

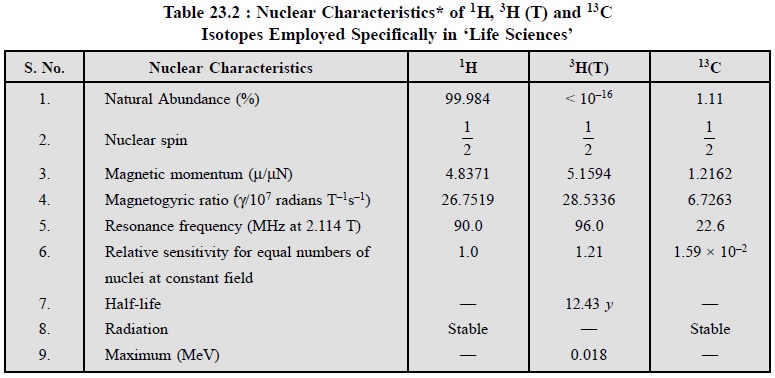
8.  ¹³C-NMR-SPECTROSCOPY

The ‘carbon-skeleton’ has been viewed directly with the help of Carbon-13 NMR spectroscopy on a particle basis since early 1970’s ; whereas ¹H-NMR spectrometry started in late 1950’s. The valuable contri-bution made by various researchers**, between 1976 and 1980, has virtually placed ¹³C-NMR to a strategi-cally much advanced stage where it gives a clear edge over ¹H-NMR in terms of not only its versatility but also its wide application in analysis.

¹³C-NMR refers to recording another NMR-spectrum but of the C-13 atoms rather than the hydrogen atoms. In actual practice, however, -‘these spectra are recorded in such a manner that each chemically dis-tinct carbon gives rise to single peak, without any coupling or fine structure’.

Hence, simply a count of the peaks can be used to see how many carbons are actually present in the molecule. But this particular technique is not reliable for a molecule that exhibits symmetry, because this would ultimately reduce the number of peaks.

It is interesting to note that ¹²C nucleus is not magnetically ‘active’ (spin quantum number I = 0), whereas the ¹³C nucleus, like the ¹H nucleus, has a spin number I =1/2  . Keeping in view the nuclear charac-teristic features one may observe that the natural abundance of ¹³C is equal to 1.1% that of ¹²C and also the sensitivity of ¹³C is equal to 1.6% that of ¹H. Therefore, the overall sensitivity of ¹³C compound with ¹H stands at 1/5700.

There are three short-comings of ¹³C-NMR spectra, namely :

1.           Only 1% of the carbon in the molecule is carbon-13,

2.           Sensitivity is consequently low, and

3.           Recording the NMR-spectra is a tedious and time consuming process. However, with the advent of recent developments in NMR-spectroscopy it is quite possible to eliminate some of these short comings adequately. They are :

(a) Development of powerful magnets (‘supercon’ magnets) has ultimately resulted in relatively stronger NMR-signals from the same number of atoms,

(b) Improved hardware in NMR-spectroscopy has gainfully accomplished higher sensitivity, and

(c) Development of more sensitive strategies has made it possible to record these C—H correla-tion spectra in a much easier manner.

Therefore, it is now possible either to record the ¹³C-NMR signal and place the hydrogens in the undetected ‘second dimension’ or to record the signal from the hydrogens and place the ¹³C resonances in the ‘indirect dimension’.

In actual practice, the latter mode is technically more demanding and affords results that are much higher in sensitivity. Recent developments in NMR-spectrometer hardware and technique have made this more-sensitive-mode of operation, termed as ‘inverse-detection’, rather readily applicable to modern analy-sis.

9.    2D-NMR (TWO DIMENSIONAL CORRELATION SPECTROSCOPY OR TWO DIMEN-SIONAL COSY SPECTRUM)

The interaction between different hydrogens in a molecule, known as ‘scaler’ or ‘spin-spin cou-pling’, transmitted invariably through chemical bonds, usually cover 2 or 3 at the most. Therefore, when a hydrogen with a chemical shift ‘A’ is coupled to a hydrogen with chemical shift ‘B’, one would immediately make out that the hydrogens must be only 2 or 3 bonds away from one another. To know exactly with particular hydrogens are coupled to one another it is necessary to record a two-dimensional ‘Correlation Spectroscopy’ (COSY) spectrum.

Generally, a normal NMR-spectrum has amplitude plotted Vs just one frequency-dimension (the ppm scale). In 2D-NMR, the amplitude is plotted Vs two frequency-dimensions (two ppm scales), normally in the form of a counter plot, just like a topographic map.

The most important aspect about these 2D-NMR spectra is that they show the relation between the peaks in an NMR-spectrum.

Example : A peak at ordinate A ppm in one dimension and B ppm in the other simply indicates that a hydrogen with shift A is duly coupled to a hydrogen with shift B. In short, this is all the information which one needs to interpret in a COSY-spectrum. Thus, the resulting chemical shifts of coupled protons may be simply read off the spectrum.

Figure 23.4, illustrates the two dimensional COSY spectrum of a sugar : 1-0-methyl α-D-glucopyranoside (1) that has been recorded on a 400 MHz NMR-spectrometer ; the sample was dissolved in D₂O so that the OH protons get duly exchanged with Deuterium and are, therefore, not seen at all. Besides, the ¹H-NMR-spectrum has also been shown alongside both axis of the two dimensional spectrum in Figure 23.4.

Salient features of ¹H-NMR and 2D-NMR spectra are, namely :

1.           At 3.25 ppm a sharp intense peak, labelled B, is characteristic of an —OMe moiety

2.           At 4.6 ppm there appears another strong peak which is due to the presence of some residual HDO in the D₂O that was initially employed to dissolve the sample,

3.           At 4.65 ppm, the two peaks or multiplets are due to H which are distinctly separated from the rest of the spectrum. These are known to belong to the aromatic proton H₁ which is present adjacent to two oxygen atoms, and

The COSY-spectrum (Figure 23.4) depicts a so called cross-peak CH at F₁ = 4.65 ppm ; F₂ = 3.4 ppm which means that the proton is coupled to another proton whose shift is 3.4 ppm.

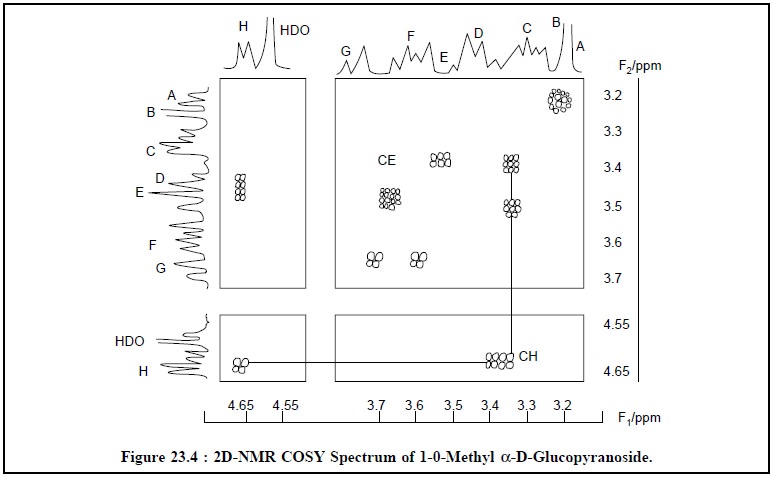
Thus, looking at the structure of compound (1), the resonance C at 3.4 ppm may be due to H₂ by connecting it to H₁.

Following along it may be observed that from multiplet C there exists another cross-peak, CE at F₁ = 3.5 ppm, F₂ = 3.4 ppm, suggesting thereby that the proton resonating at 3.4 ppm is duly coupled to one resonating at 3.5 ppm ; this identifies multiplet E as H₃. In fact, from this single COSY-spectrum (Figure 23.4) one may identify the complete chain of coupled protons as it goes round the pyranose ring.

However, in actual practice with a little skill and expertise one may :

(i) Read off the bonding network from the spectrum,

(ii) Interpret a COSY spectra easily, because without it finding the coupled pairs of hydrogens is mostly not only ambiguous but also time-consuming, and

(iii) Reveal a few chains of coupled resonances.