Multiple Encryption and Triple DES(Data Encryption Standard)

MULTIPLE ENCRYPTION AND TRIPLE DES

Given the potential vulnerability of DES to a brute-force attack, there has been considerable interest in finding an alternative. One approach is to design a completely new algorithm, of which AES is a prime example. Another alternative, which would preserve the existing investment in software and equipment, is to use multiple encryption with DES and multiple keys. We begin by examining  the simplest example of this second alternative. We then look at the widely accepted triple DES (3DES) approach.

Double DES

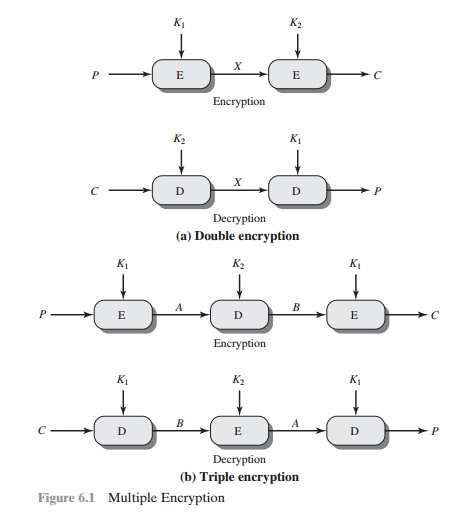
The simplest form of multiple encryption has two encryption stages and two keys (Figure 6.1a). Given a plaintext P and two encryption keys K1 and K2, ciphertext C is generated as

C  = E(K2, E(K1, P))

Decryption requires that the keys be applied in reverse order:

P  = D(K1, D(K2, C))

For DES, this scheme apparently involves a key length of 56 * 2 = 112 bits, result- ing in a dramatic increase in cryptographic strength. But we need to examine the algorithm more closely.

REDUCTION TO A SINGLE STAGE Suppose it were true for DES, for all 56-bit key values, that given any two keys K1 and K2, it would be possible to find a key K3 such  that

E(K2, E(K1, P))  = E(K3, P)                       (6.1)

If this were the case, then double encryption, and indeed any number of stages of multiple encryption with DES, would be useless because the result would be equiv- alent to a single encryption with a single 56-bit key.

On the face of it, it does not appear that Equation (6.1) is likely to hold. Consider that encryption with DES is a mapping of 64-bit blocks to 64-bit blocks. In fact, the mapping can be viewed as a permutation. That is, if we consider all 264 pos- sible input blocks, DES encryption with a specific key will map each block into a unique 64-bit block. Otherwise, if, say, two given input blocks mapped to the same output block, then decryption to recover the original plaintext would be impossible. With 264 possible inputs, how many different mappings are there that generate a permutation of the input blocks? The value is easily seen to be

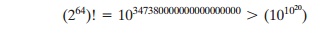
On the other hand, DES defines one mapping for each different key, for a total number of mappings:

256  6 1017

Therefore, it is reasonable to assume that if DES is used twice with different keys, it will produce one of the many mappings that are not defined by a single application of DES. Although there was much supporting evidence for this assumption, it was not until 1992 that the assumption was proven [CAMP92].

MEET-IN-THE-MIDDLE ATTACK Thus, the use of double DES results in a mapping that is not equivalent to a single DES encryption. But there is a way to attack this scheme, one that does not depend on any particular property of DES but that will work against any block encryption cipher.

The algorithm, known as a meet-in-the-middle attack, was first described in [DIFF77]. It is based on the observation that, if we  have

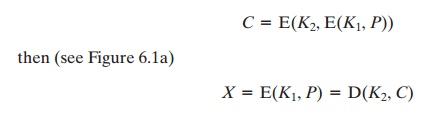
Given a known pair, (P, C), the attack proceeds as follows. First, encrypt P for all 256 possible values of K1. Store these results in a table and then sort the table by the values of X. Next, decrypt C using all 256 possible values of K2. As each decryption is produced, check the result against the table for a match. If a match occurs, then test the two resulting keys against a new known plaintext–ciphertext pair. If the two keys produce the correct ciphertext, accept them as the correct keys.

For any given plaintext P, there are 264 possible ciphertext values that could be produced by double DES. Double DES uses, in effect, a 112-bit key, so   that there are 2112 possible keys. Therefore, on average, for a given plaintext P,  the

number of different 112-bit keys that will produce a given ciphertext C is

2112/264 = 248. Thus, the foregoing procedure will produce about 248 false alarms on the first (P, C) pair. A similar argument indicates that with an additional 64 bits of known plaintext and ciphertext, the false alarm rate is reduced to 248 - 64 = 2 - 16. Put another way, if the meet-in-the-middle attack is performed on two blocks of known plaintext–ciphertext, the probability that the correct keys are determined  is 1 - 2 - 16. The result is that a known plaintext attack will succeed against double DES, which has a key size of 112 bits, with an effort on the order of 256, which is not much more than the 255 required for single DES.

Triple DES with Two  Keys

An obvious counter to the meet-in-the-middle attack is to use three stages of encryption with three different keys. This raises the cost of the meet-in-the-middle attack to 2112, which is beyond what is practical now and far into the future. However, it has the drawback of requiring a key length of 56 * 3 = 168 bits, which may be somewhat unwieldy.

As an alternative, Tuchman proposed a triple encryption method that uses only two keys [TUCH79]. The function follows an encrypt-decrypt-encrypt (EDE) sequence (Figure 6.1b):

C  = E(K1, D(K2, E(K1, P)))

P  = D(K1, E(K2, D(K1, C)))

There is no cryptographic significance to the use of decryption for the second stage. Its only advantage is that it allows users of 3DES to decrypt data encrypted by users of the older single DES:

C  = E(K1, D(K1, E(K1, P)))  = E(K1, P)

P  = D(K1, E(K1, D(K1, C)))  = D(K1, C)

3DES with two keys is a relatively popular alternative to DES and has been adopted for use in the key management standards ANS X9.17 and ISO 8732.1

Currently, there are no practical cryptanalytic attacks on 3DES. Coppersmith [COPP94] notes that the cost of a brute-force key search on 3DES is on the order of 2112 L (5 * 1033) and estimates that the cost of differential cryptanalysis suffers an exponential growth, compared to single DES, exceeding 1052.

It is worth looking at several proposed attacks on 3DES that, although not practical, give a flavor for the types of attacks that have been considered and that could form the basis for more successful future attacks.

The first serious proposal came from Merkle and Hellman [MERK81]. Their plan involves finding plaintext values that produce a first intermediate value of A = 0

(Figure 6.1b) and then using the meet-in-the-middle attack to determine the two keys. The level of effort is 256, but the technique requires 256 chosen plaintext–ciphertext pairs, which is a number unlikely to be provided by the holder of the keys.

A known-plaintext attack is outlined in [VANO90]. This method is an improvement over the chosen-plaintext approach but requires more effort. The attack is based on the observation that if we know A and C (Figure 6.1b), then the problem reduces to that of  an  attack on  double DES. Of  course,  the attacker does not know A, even if P and C are known, as long as the two keys are unknown. However, the attacker can choose a potential value of A and then try to find a known (P, C) pair that produces A. The attack proceeds as   follows.

1.      Obtain n (P, C) pairs. This is the known plaintext. Place these in a table (Table 1) sorted on the values of P (Figure 6.2b).

2.      Pick an arbitrary value a for A, and create a second table (Figure 6.2c) with entries defined in the following fashion. For each of the 256 possible keys K1 = i, calculate the plaintext value Pi that produces a:

Pi  =  D(i, a)

For each Pi that matches an entry in Table 1, create an entry in Table 2 consisting of the K1 value and the value of B that is produced for the (P, C) pair from Table 1, assuming that value of K1:

B  = D(i, C)

At the end of this step, sort Table 2 on the values of B.

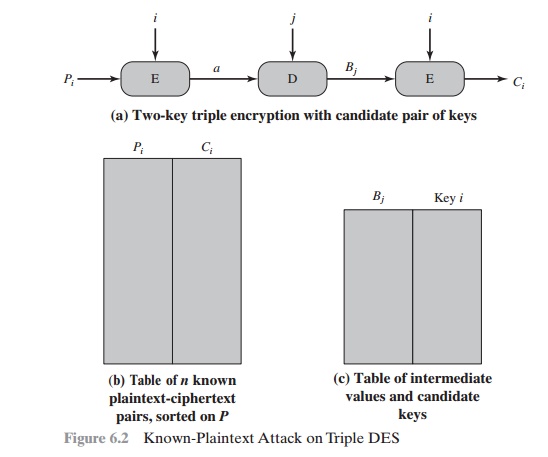
1.         We now have a number of candidate values of K1 in Table 2 and are in a position to search for a value of K2. For each of the 256 possible keys K2 = j, calculate the second intermediate value for our chosen value of a:

Bj  =  D(j, a)

At each step, look up Bj in Table 2. If there is a match, then the corresponding key i from Table 2 plus this value of j are candidate values for the unknown keys (K1, K2). Why? Because we have found a pair of keys (i, j) that produce a known (P, C) pair (Figure 6.2a).

2.         Test each candidate pair of keys (i, j) on a few other plaintext–ciphertext pairs. If a pair of keys produces the desired ciphertext, the task is complete. If no pair succeeds, repeat from step 1 with a new value of a.

For a given known (P, C), the probability of selecting the unique value of a that leads to success is 1/264. Thus, given n (P, C) pairs, the probability of success for a single selected value of a is n/264. A basic result from probability theory is that the expected number of draws required to draw one red ball out of a  bin containing n red balls and N - n green balls is (N + 1)/(n  + 1) if the balls are not replaced. So the expected number of values of a that must be tried is, for large n,

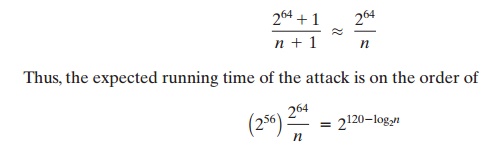
Triple DES with Three Keys

Although the attacks just described appear impractical, anyone using two-key 3DES may feel some concern. Thus, many researchers now feel that three-key 3DES is the preferred alternative (e.g., [KALI96a]). Three-key 3DES has an effective key length of 168 bits and is defined as

C  = E(K3, D(K2, E(K1, P)))

Backward compatibility with DES is provided by putting K3  =  K2 or K1  =   K2.

A number of Internet-based applications have adopted three-key 3DES, including PGP and S/MIME, both discussed in Chapter 18.