Cipher Block Chaining(CBC) Mode

CIPHER BLOCK CHAINING MODE

To overcome the security deficiencies of ECB, we would like a technique in which the same plaintext block, if repeated, produces different ciphertext blocks. A simple way to satisfy this requirement is the cipher block chaining (CBC) mode (Figure 6.4). In this scheme, the input to the encryption algorithm is the XOR of the current plain- text block and the preceding ciphertext block; the same key is used for each block. In effect, we have chained together the processing of the sequence of plaintext blocks. The input to the encryption function for each plaintext block bears no fixed relation- ship to the plaintext block. Therefore, repeating patterns of b bits are not exposed. As with the ECB mode, the CBC mode requires that the last block be padded to a full b bits if it is a partial block.

For decryption, each cipher block is passed through the decryption algorithm. The result is XORed with the preceding ciphertext block to produce the plaintext block. To see that this works, we can write

Cj = E(K, [Cj - 1 Ⓧ Pj])

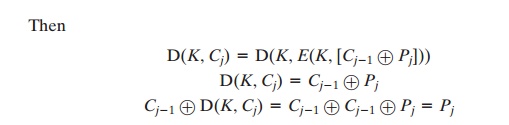
To produce the first block of ciphertext, an initialization vector (IV) is XORed with the first block of plaintext. On decryption, the IV is XORed with the output of the decryption algorithm to recover the first block of plaintext. The IV is a data block that is that same size as the cipher block. We can define CBC mode as

The IV must be known to both the sender and receiver but be unpredictable by a third party. In particular, for any given plaintext, it must not be possible to pre- dict the IV that will be associated to the plaintext in advance of the generation of the IV. For maximum security, the IV should be protected against unauthorized changes. This could be done by sending the IV using ECB encryption. One reason for protecting the IV is as follows: If an opponent is able to fool the receiver into using a different value for IV, then the opponent is able to invert selected bits in the first block of plaintext. To see this, consider

C1 = E(K, [IV Ⓧ P1]) 

P1  = IV Ⓧ D(K, C1)

Now use the notation that X[i] denotes the ith bit of the b-bit quantity X. Then

P1[i]  =  IV[i] Ⓧ D(K, C1)[i]

Then, using the properties of XOR, we can state

P1[i]' =  IV[i]' Ⓧ D(K, C1)[i]

where the prime notation denotes bit complementation. This means that if an oppo- nent can predictably change bits in IV, the corresponding bits of the received value of P1 can be changed.

For other possible attacks based on prior knowledge of IV, see [VOYD83].

So long as it is unpredictable, the specific choice of IV is unimportant. Sp800-38a recommends two possible methods: The first method is to apply the encryption function, under the same key that is used for the encryption of the plain- text, to a nonce.2 The nonce must be a data block that is unique to each execution of the encryption operation. For example, the nonce may be a counter, a timestamp, or a message number. The second method is to generate a random data block using a random number generator.

In conclusion, because of the chaining mechanism of CBC, it is an appropriate mode for encrypting messages of length greater than b   bits.

In addition to its use to achieve confidentiality, the CBC mode can be used for authentication. This use is described in Chapter 12.