Mechanical Translational systems

Mechanical Translational systems

The model of mechanical translational systems can obtain by using three basic elements mass, spring and dashpot. When a force is applied to a translational mechanical system, it is opposed by opposing forces due to mass, friction and elasticity of the system. The force acting on a mechanical body is governed by Newton‗s second law of motion. For translational systems it states that the sum of forces acting on a body is zero.

Force balance equations of idealized elements:

 1.

Consider an ideal mass element shown in fig. which has negligible friction and elasticity. Let a force be applied on it. The mass will offer an opposing force which is proportional to acceleration of a body.

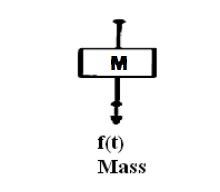
Let f = applied force

fm =opposing force due to mass Here

fm α M d2 x / dt2

By Newton's second law, f = f m= M d2 x / dt2

2.

Consider an ideal frictional element dash-pot shown in fig. which has negligible mass and elasticity. Let a force be applied on it. The dashpot will be offer an opposing force which is proportional to velocity of the body.

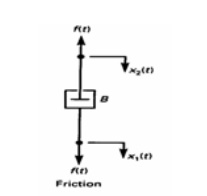
Let f = applied force

f b = opposing force due to friction

Here, f b α B dx / dt

By Newton's second law, f = fb = M d x / dt

3.

Consider an ideal elastic element spring is shown in fig. This has negligible mass and friction.

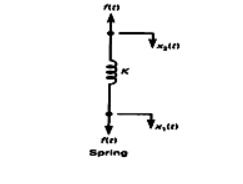
Let f = applied force

f k = opposing force due to elasticity

Here, f k α x

By Newtons second law, f = f k = x