Mechanical Rotational Systems

Mechanical Rotational Systems:

The model of rotational mechanical systems can be obtained by using three elements, moment of inertia [J] of mass, dash pot with rotational frictional coefficient [B] and torsional spring with stiffness[k].

When a torque is applied to a rotational mechanical system, it is opposed by opposing torques due to moment of inertia, friction and elasticity of the system. The torque acting on rotational mechanical bodies is governed by Newton’s second law of motion for rotational systems.

Torque balance equations of idealized elements

1. 

Consider an ideal mass element shown in fig. which has negligible friction and elasticity. The opposing torque due to moment of inertia is proportional to the angular acceleration.

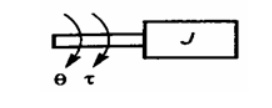
Let T = applied torque

Tj =opposing torque due to moment of inertia of the body

Here Tj= α J d2 θ / dt2

By Newton‗s law

T= Tj = J d2 θ / dt2

2.  

Consider an ideal frictional element dash pot shown in fig. which has negligible moment of inertia and elasticity. Let a torque be applied on it. The dash pot will offer an opposing torque is proportional to angular velocity of the body.

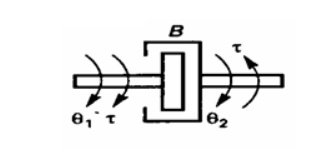
Let T = applied torque

Tb =opposing torque due to friction

Here Tb = α B d / dt (θ1- θ2)

By Newton‗s law

T= Tb = B d / dt (θ1- θ2)

3.  

. Consider an ideal elastic element, torsional spring as shown in fig. which has negligible moment of inertia and friction. Let a torque be applied on it. The torsional spring will offer an opposing torque which is proportional to angular displacement of the body

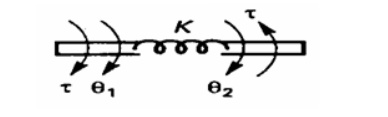
Let T = applied torque

Tk =opposing torque due to friction

Here Tk α K (θ1- θ2)

By Newton‗s law

T = Tk = K (θ1- θ2)