Magnetic Circuit Analysis on Open Circuit

MAGNETIC CIRCUIT ANALYSIS ON OPEN CIRCUIT

Cross section of a 2 pole brushless dc motor having high energy rare earth magnets on the rotor and the demagnetization curve are as shown in fig 4.32 (a & b)

First step to analyze a magnetic circuit is to identify the main flux paths and the reluctance or permeances assigned to them.

The equivalent magnetic circuit is shown in fig 4.33.only half of the equivalent circuit is shown & the lower half is the mirror image of the upper half about the horizontal axis, which is at equipotential. This assumption is true only if the two halves are balanced. If not the horizontal axis might still be an equipotential but the fluxes and the magnetic potentials in the two halves would be different and there could be residual flux in the axial direction .along the shaft. The axial flux is undesirable because it can induce current to flow in the bearing.

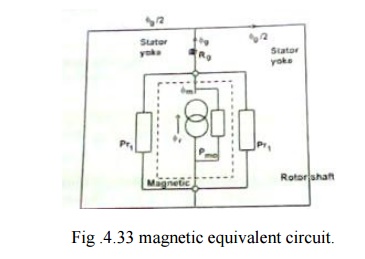
The steel cores of the stator and rotor shaft are assumed to be infinitely permeable.

Each magnet is represented by a ‗Norton‘ equivalent circuit consisting of a flux generator in parallel with an internal leakage permeance p_mo.

υr=BrAm    …….(4.43)

Pmo=μ0μrecAm/lm        …….(4.44)

where  Am – pole area the magnet   

lm – length of the magnet in the direction of magnetization (in this case its radial thickness)

Br- remanent flux density

μrec- relative recoil permeability (the slope of the demagnetization curve)

In this case the outer pole area is larger than the inner pole area but to keep the analysis simple average pole area is considered.

with a magnet arc of 120°

Am=2/3^ᴨ[r1–g-lm/2]l                                                          ……….(4.45)

r1- radius of the rotor

g- air gap length

most of the magnet flux crosses the air gap via the air gap reluctance Rg

Rg=g‘/μ0Ag          ………..(4.46)

g‘- equivalent air gap length allowing for slotting.

the slotting can be taken into account by means of carter‘s coefficient, which case,

g‘=Kc g                                                                    ………………………...(4.47)

Ag- air gap area through which the flux passes as it crosses he gap . the precise boundary of this area is uncertain because of fringing both at the edges of the magnet and at the ends of the rotor.An approximate allowance for fringing can be made by adding ‗g‘ at each of the four boundaries ,giving

Ag=[2/3   (r1- g/2)+2g](l+2g) …..(4.48)

       the remaining permeance in the magnetic circuit I the rotor leakage permeance ρrl, which represents the paths of the magnet flux components that fails to cross the air gap. this can be conveniently included in a modified magnet internal permeance by writing

pm=pmo+prl       …………(4.49(a))

pm=pmo(1+prl)   …….(4.49(b))

prl-normalized rotor leakage permeance