Emf Equation of BLPM SQW DC Motors

EMF EQUATION OF BLPM SQW DC MOTORS

The basic torque emf equations of the brushless dc motor are quite simple and resemble those of the dc commutator motor.

The co-ordinate axis have been chosen so that the center of a north pole of the magnetic is aligned with the x-axis at Ó¨ = 0 .the stator has 12 slots and a three phasing winding. Thus there are two slots per pole per phase.

^v   Consider a BLPM SQW DC MOTOR

Let ‘p‘be the number of poles (PM)

‘B_g‘ be the flux density in the air gap in wb/m².

B_k is assumed to be constant over the entire pole pitch in the air gap (180^ÔŽ pole arc)

‘r‘ be the radius of the airgap in m.

‘l‘ be the length of the armature in m.

‘T_c‘ be the number of turns per coil.

‘ω_m‘ be the uniform angular velocity of the rotor in mechanical rad/sec.

ω_m=2πN/60 where N is the speed in rpm.

Flux density distribution in the air gap is as shown in fig 4.14.At t=0(it is assumed that the axis of the coil coincides with the axis of the permanent magnet at time t=0).

Let at ω_mt=0,the centre of N-pole magnet is aligned with x-axis.

At ω_mt=0,x-axis is along PM axis.

Therefore flux enclosed by the coli is

Φ_max=B x 2Ï€r/p x l                                          ………………...(4.1)

=flux/pole

Φ_max=rl∫₀^Ï€ B(θ)dθ

=B_g rl[θ]₀^Ï€

=B_grl[Ï€]

At ω_mt=0,the flux linkage of the coil is

Λ_max= (B_g x 2Ï€r/p x l)T_c ωb-T                                     …………………….(4.2)

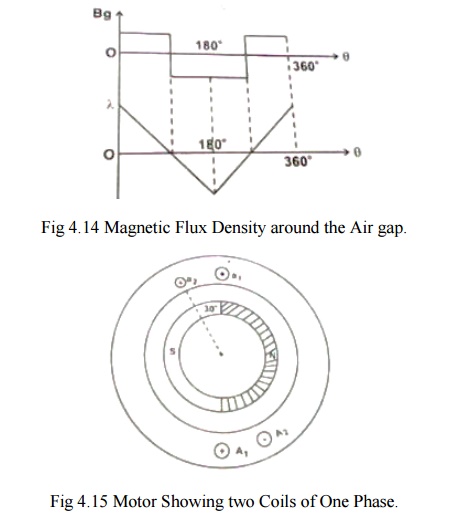
Let the rotor rotating in ccw direction and when ω_mt=π/2, the flux enclosed by the coil Φ, Therefore λ=0.

The flux linkages of the coil vary with θ variation of the flux linkage is as shown above.

The flux linkages of the coil changes from B_grlTcπ/p at ω_mt=0 (i.e) t= 0 t0 θ at t=π/pω_m.

Change of flux linkage of the coil (i.e) ∆λ is

∆λ/∆t =Final flux linkage – Initial flux linkage/time.

=0- (2B_grlTcπ/p)/ (π/pω_m)

= -(2B_grlTcω_m)                                          …………………………...(4.3)

The emf induced in the coil e_c= - dλ/dt

e_c =2B_grlTcω_m                                             …………………………….(4.4)

Distribution of e_c with respect to t is shown in fig 4.16

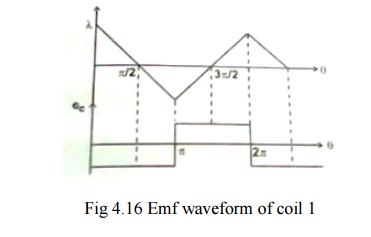
It is seen that the emf waveform is rectangular and it toggles between + e_c to - e_c. The period of the wave is 2πr/pω_m sec and magnitude of e_c is

e_c =2B_grlTcω_m  volts                             ………………………………...(4.5)

Consider two coils a1A1 and a2A2 as shown in fig 5.15.Coil a2A2 is adjacent to a1A1 is displaced from a1A1 by an angle 30^ÔŽ(i.e.) slot angle Ï’ .

The magnitude of emf induced in the coil a1A1

e_c2 =B_grlTcω_m volts                   …………………………….(4.6)

The magnitude of emf induced in the coil a2A2

e_c2 =B_grlTcω_m volts                       …………………………...(4.7)

Its emf waveform is also rectangular but displaced by the emf of waveform of coil e_c1 by slot angle Ï’ .

If the two coils are connected in series, the total phase voltage is the sum of the two separate coil voltages.

e_c1      +e_c2 =2B_grlTcω_m   ………………………………..(4.8)

Let nc          be the number of coils that are connected in series per phase   n_cT_c  =T_ph  be the

number of turns/phase. 

e_ph= n_c [2B_grlTcω_m ]       ……………………………….(4.9)

e_ph= 2B_grlTphωm volts  ………………………………..(4.10)

e_ph=resultant emf when all nc coils are connected in series.

The waveforms are as shown in fig 4.17

The waveform of e_ph is stepped and its amplitude is 2B_grlTphω_m volts.

At any instant 2-phase windings are connected in series across the supply terminals as shown in fig 4.18.

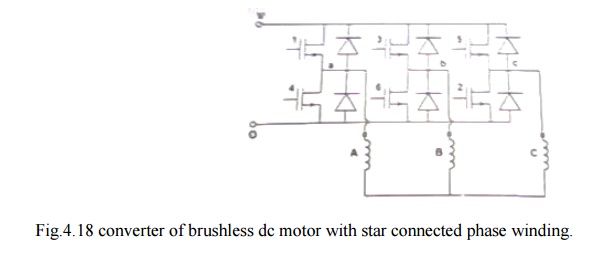
Assumption

Armature winding is Y connected.

Electronic switches are so operated using rotor position sensor that the resultant emfs across the winding terminals is always = 2 eph.

Amplitude of back emf generated in Y connected armature winding E = 2 eph.