Chapter: Operations Research: An Introduction : Deterministic Dynamic Programming
Knapsack/Fly-Away/Cargo Loading Model- Dynamic Programming(DP) Applications
Knapsack/Fly-Away/Cargo-Loading
Model
The
knapsack model classically deals with the situation in which a soldier (or a
hiker) must decide on the most valuable items to carry in a backpack. The
problem paraphrases a general resource allocation model in which a single
limited resource is assigned to a number of alternatives (e.g., limited funds
assigned to projects) with the objective of maximizing the total return.
Before
presenting the DP model, we remark that the knapsack
problem is also known in the literature as the fly-away kit problem, in which a jet pilot must determine the most
valuable (emergency) items to take aboard a jet; and the cargo-loading prob-lem, in which a vessel with limited volume or
weight capacity is loaded with the most valuable cargo items. It appears that the three names
were coined to ensure equal rep-resentation of three branches of the armed
forces: Air Force, Army, and Navy!
The
(backward) recursive equation is developed for the general problem of an n-item
W-Ib
knapsack. Let mi be the
number of units of item i in the knapsack and define ri and wi as the revenue and weight per unit of item i. The general problem is represented by
the following ILP:


Step 2. Express xi+1 as a function of xi to ensure that the left-hand side, fi(xi),
is a function of xi only. By
definition, xi - xi+1 = wimi represents the weight used at stage i. Thus, xi+1 = xi
- wimj, and the
proper recursive equation is given as
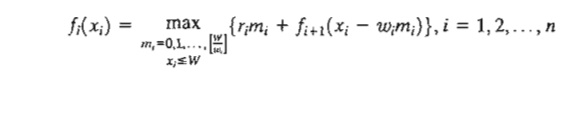
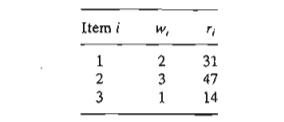
Example
10.3-1
A 4-ton
vessel can be loaded with one or more of three items. The following table gives
the unit weight, wi, in tons and the unit revenue in
thousands of dollars, ri,
for item i. How should the vessel be
loaded to maximize the total return?
Because
the unit weights wi and the maximum weight W are integer, the state xi assumes
integer values only.
Stage 3. The exact weight to be allocated
to stage 3 (item 3) is not known in advance, but can assume one of the values
0,1, ... , and 4 (because W = 4
tons). The states x3 = and x3 = 4, respectively, represent the
extreme cases of not shipping item 3 at all and of allocating the entire vessel
to it. The remaining values of x3 (= 1,2, and 3) imply a partial
allocation of the vessel capacity to item 3. In effect, the given range of
values for x3 covers all possible allocations of the vessel
capacity to item 3.
Given w3 = 1 ton per unit, the maximum number of units
of item 3 that can be loaded is
4/l = 4, which
means that the possible values of
m3 are 0,
1,2,3, and 4. An alternative m3 is feasible
only if w3m3 ≤ x3. Thus, all the infeasible
alternatives (those for which w3m3 > x3 ) are
excluded. The following equation is the basis for comparing the alternatives of
stage 3.
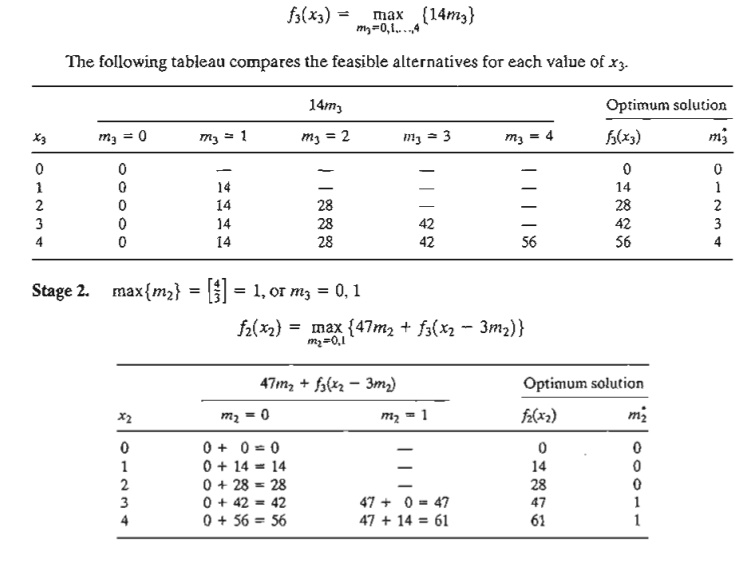

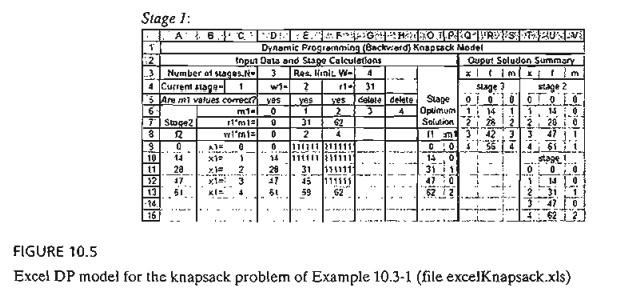
The
optimum solution is determined in the following manner: Given W = 4 tons,
from stage 1, x1 = 4 gives the optimum alternative
mi* = 2, which means that 2 units of item 1 will be loaded on the
vessel. This allocation leaves x2
= x1 - 2m2* = 4
- 2 X 2 = 0. From stage 2, x2 = 0 yields m2* = 0, which, in turn, gives x3 = x2 - 3m2 = 0 - 3 X 0 = 0. Next, from stage 3, x3 = 0 gives m3* = 0. Thus, the complete optimal solution is mi* = 2, m2* = 0, and m3* = 0. The associated return
is f1(4) =
$62,000.
In the
table for stage 1, we actually need to obtain the optimum for xl = 4 only because this is the last
stage to be considered. However, the computations for x1 = 0, 1, 2, and 3 are induded to
allow carrying out sensitivity analysis.
For example, what happens if the vessel capacity is 3 tons in place of 4 tons?
The new optimum solution can be determined as
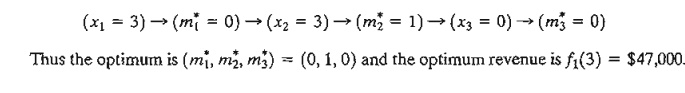
Remarks. The cargo-loading example
represents a typical resource allocation
model in which a limited resource is apportioned among a finite number of
(economic) activities. The objective maximizes an associated return function.
In such models, the definition of the state at each stage will be similar to
the definition given for the cargo-loading model. Namely, the state at stage i is the total resource amount allocated
to stages i, i + 1, ... , and n.
Excel
moment
The
nature of dynamic programming computations makes it impossible to develop a
general computer code that can handle all DP problems. Perhaps this explains
the persistent absence of commercial DP software.
In this
section, we present a Excel-based algorithm for handling a subclass of DP
problems: the single-constraint knapsack problem (file Knapsack.xls). The algorithm
is not data specific and can handle problems in this category with 10 alternatives
or less.
Figure
10.4 shows the starting screen of the knapsack (backward) DP model. The screen
is divided into two sections: The right section (columns Q:V) is used to summarize
the
output solution. In the left section (columns A:P), rows 3,4, and 6 provide the
input data for the current stage, and rows 7 and down are reserved for stage
computations. The input data symbols correspond to the mathematical notation in
the DP model, and are self-explanatory. To fit the spreadsheet conveniently on
one screen, the maximum feasible value for alternative mi at stage
i is 10
(cells D6:N6).
Figure
10.5 shows the stage computations generated by the algorithm for Example
10.3-1. The computations are carried out one stage at a time, and the user
provides the basic data that drive each stage. Engaging you in this manner will
enhance your understanding of the computational details in DP
Starting
with stage 3, and using the notation and data in Example 10.3-1, the input
cells are updated as the following list shows:
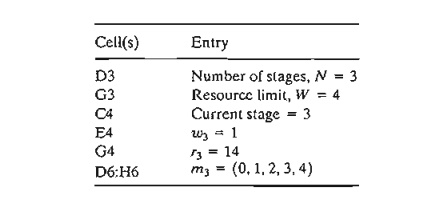
Note that
the feasible values of m3
are 0, 1, ... , and [W/w3] = [4/1] = 4, as in Example 10.3-1. The
spreadsheet automatically tells you how many m3 values are needed
and checks the validity of the values you enter by issuing self-explanatory
messages in row 5: "yes," "no," and "delete." ..
,
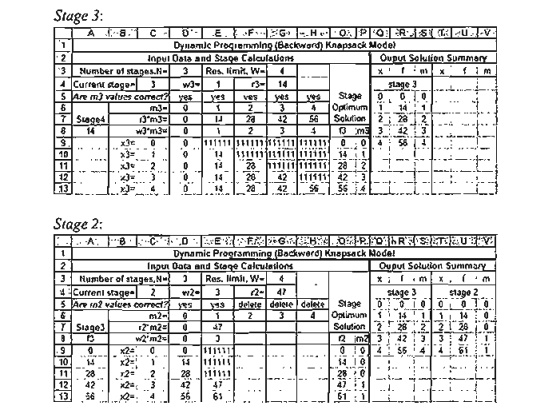
As stage
3 data are entered and verified, the spreadsheet will "come alive"
and will generate all the necessary computations of the stage (columns B
through P) automatically. The value -1111111 is used to indicate that the
corresponding entry is not feasible. The optimum solution (f3, m3)
for the stage is given in columns 0 and P Column A provides the values of f4- Because the computations
start at stage 3,f4 = 0 for all values of x3. You can
leave A9:A13 blank or enter all zero values.
Now that
stage 3 calculations are at hand, take the following steps to create a permanent record of the optimal solution
of the current stage and to prepare the spread-sheet for next stage
calculations:
Step 1. Copy the x3-values,
C9:C13, and paste them in Q5:Q9 in the optimum solution summary section. Next,
copy the (f3, m3)-values, 09:P13, and paste them in
R5:S9. Remember that you need to paste values only, which requires selecting Paste Special from Edit menu and Values from the dialogue box.
Step 2. Copy
the f3-values in R5:R9 and
paste them in A9:A13 (you do not need
Paste Special in this step).
Step 3. Change cell C4 to 2 and enter the
new values of w2, r2, and m2 to record the data of stage 2. .
Step 2
places fi+1(xi -
wimi) in column
A in preparation for calculating fi(xi)
at stage i (see the recursive formula for the knapsack problem in Example 10.3-1).
This explains the reason for entering zero values, representing f4, in column A of stage 3
tableau,
Once
stage 2 computations are available, you can prepare the screen for stage 1 in a
similar manner. When stage 1 is complete, the optimum solution summary can be
used to read the solution, as was explained in Example 10.3-1. Note that the
organization of the output solution summary area (right section of the screen,
columns Q:V) is free-formatted and you can organize its contents in any
convenient manner you desire.
PROBLEM SET 10.3A
1. In Example 10.3-1, determine the optimum solution, assuming that the
maximum weight capacity of the vessel is 2 tons then 5 tons.
2. Solve the cargo-loading problem of Example 10.3-1 for each of the
following sets of data:
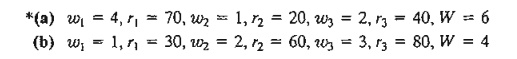
3. In the cargo-loading model of Example 10.3-1, suppose that the
revenue per item includes a constant amount that is realized only if the item
is chosen, as the following table shows:

Find the optimal solution using DP. (Hint:
You can use the Excel file excelSetupKnapsack.xls to check your calculations.)
4. A
wilderness hiker must pack three items: food, first-aid kits, and clothes. The
backpack has a capacity of 3 ft3. Each unit of food takes 1 ft3. . A
first-aid kit occupies V4 ft3 and each piece of cloth takes about 1/2ft3. The hiker assigns the priority weights 3,4, and 5 to food, first aid, and
clothes, which means that clothes are the most valuable of the three items.
From experience, the hiker must take at least one unit of each item and no more
than two first-aid kits. How many of each item should the hiker take?
*5. A
student must select 10 electives from four different departments, with at least
one course from each department. The 10 courses are allocated to the four
departments in a manner that maximizes "knowledge." The student
measures knowledge on a l00-point scale and comes up with the following chart:
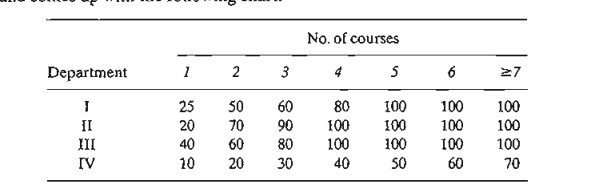
How
should the student select the courses?
6. I have
a small backyard garden that measures 10 X 20 feet.
This spring I plan to plant three types of vegetables: tomatoes, green beans,
and corn. The garden is organized in 10-foot ro\ys. The corn and tomatoes rows
are 2 feet wide, and the beans rows are 3 feet wide. I like tomatoes the most
and beans the least, and on a scale of 1 to 10, I would assign 10 to tomatoes,
7 to corn, and 3 to beans. Regardless of my preferences, my wife insists that I
plant at least one row of green beans and no more than two rows of toma-toes.
How many rows of each vegetable should I plant?
*7.
Habitat for Humanity is a wonderful charity organization that builds homes for
needy fami-lies using volunteer labor. An eligible family can chose from three
home sizes: 1000, 1100, and 1200 ft2. Each
size house requires a certain number of labor volunteers. The Fayetteville
chapter has received five applications for the upcoming 6 months. The
commit-tee in charge assigns a score to each application based on several
factors. A higher score sig-nifies more need. For the next 6 months, the
Fayetteville chapter can count on a maximum of 23 volunteers. The following
data summarize the scores for the applications and the required number of
volunteers. Which applications should the committee approve?
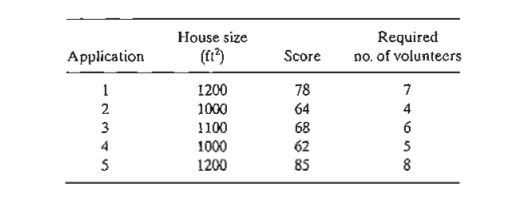
8. Sheriff
Bassam is up for reelection in Washington county. The funds available for the
campaign are about $10,000. Although the reelection committee would like to
launch the campaign in all five precincts of the county, limited funds dictate
otherwise. The following table lists the voting population and the amount of
funds needed to launch an effective campaign in each precinct. The choice for
each precinct is to receive either all allotted funds or none. How should the
funds be allocated?
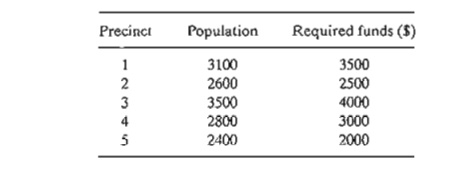
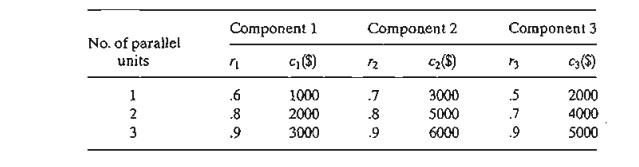
9. An
electronic device consists of three components. The three components are in
series so that the failure of one component causes the failure of the device.
The reliability (probability of no failure) of the device can be improved by
installing one or two standby units in each component. The following table
charts the reliability, r, and the cost, c. The total capital available for the
construction of the device is $10,000. How 10.3
should the device be constructed? (Hint:
The objective is to maximize the reliability, r1r2r3, of the
device. This means that the decomposition of the objective function is
multi-plicative rather than additive.)
10. Solve
the following model by DP:
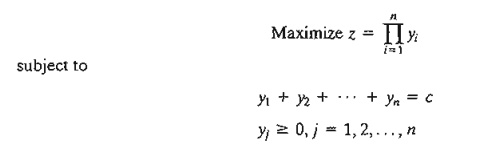
(Hint: This problem is similar to
Problem 9, except that the variables, yi,
are continuous.)
11. Solve
the following problem by DP:

Related Topics