Investment Model- Dynamic Programming(DP) Applications

Investment Model

Suppose that you want to invest the amounts Pi, P2, ..... , pn at the start of each of the next n years. You have two investment opportunities in two banks: First Bank pays an interest rate r1 and Second Bank pays r2, both compounded annually. To encourage deposits, both banks pay bonuses on new investments in the form of a percentage of the amount invested. The respective bonus percentages for First Bank and Second Bank are qi1 and qi2 for year i. Bonuses are paid at the end of the year in which the investment is made and may be reinvested in either bank in the immediately succeeding year. This means that only bonuses and fresh new money may be invested in either bank. However, once an investment is deposited, it must remain in the bank until the end of the n-year horizon. Devise the investment schedule over the next n years.

The elements of the DP model are

a.     Stage i is represented by year i, i =  1, 2, ... , n.

b.     The alternatives at stage i are Bar(Ii) and ~, the amounts invested in First Bank and Second Bank, respectively.

c.      The state, xi, at stage i is the amount of capital available for investment at the start of year i.

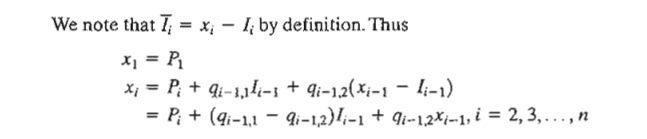
The reinvestment amount xi includes only new money plus any bonus from investments made in year i - l.

Define

fi(xi) = optimal value of the investments for years i, i + 1, ... , and n, given xi Next, define si as the accumulated sum at the end of yearn, given that Ii and (xi - Ii) are the investments made in year i in First Bank and Second Bank, respectively. Letting ak = (1 + rk), k =1,2, the problem can be stated as

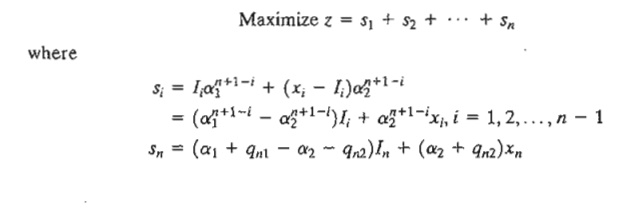
The terms qn1 and qn2 in Sn are added because the bonuses for year n are part of the final accumulated sum of money from the investment.

The backward DP recursive equation is thus given as

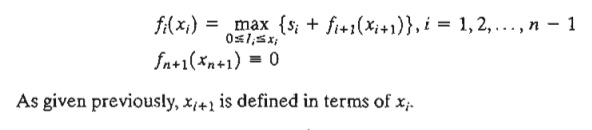
Example 10.3-4

Suppose that you want to invest $4000 now and $2000 at the start of years 2 to 4. The interest rate offered by First Bank is 8% compounded annually, and the bonuses over the next 4 years are 1.8%,1.7%,2.1%, and 2.5%, respectively. The annual interest rate offered by Second Bank is .2% lower than that of First Bank, but its bonus is .5% higher. The objective is to maximize the accumulated capital at the end of 4 years.

Using the notation introduced previously, we have

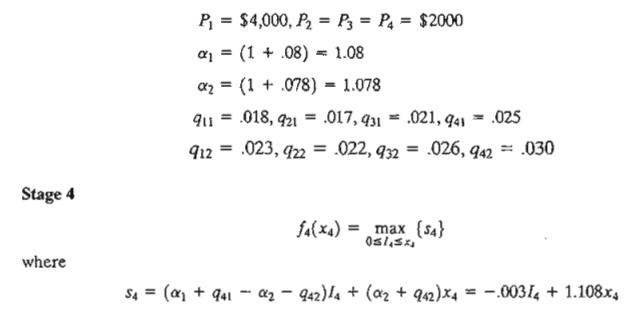
The function s4 is linear in I4 in the range 0 ≤ I4 ≤ x4 and its maximum occurs at 14 = 0 because of the negative coefficient of I4 Thus, the optimum solution for stage 5 can be summarized as

PROBLEM SET 10.30

1. Solve Example 10.3-4, assuming that r1 = .085 and r2 = .08. Additionally, assume that P1 = $5000, P2 = $4000, P3 =: $3000, and P4 = $2000.

2. An investor with an initial capital of $10,000 must decide at the end of each year how much to spend and how much to invest in a savings account. Each dollar invested returns a = $1.09 at the end of the year. The satisfaction derived from spending $y in anyone year is quantified by the equivalence of owning $Root(Y). Solve the problem by DP for a span of5 years.

3. A farmer owns k sheep. At the end of each year, a decision is made as to how many to sell or keep. The profit from selling a sheep in year i is pi. The sheep kept in year i will double in number in year i + 1. The farmer plans to sell out completely at the end of n years.

*a. Derive the general recursive equation for the problem.

b. Solve the problem for n = 3 years, k = 2 sheep, P1 = $100, P2 = $130. and P3 = $120.