Equipment Replacement Model- Dynamic Programming(DP) Applications

Equipment Replacement Model

The longer a machine stays in service, the higher is its maintenance cost, and the lower its productivity. When a machine reaches a certain age, it may be more economical to replace it. The problem thus reduces to determining the most economical age of a machine.

Suppose that we are studying the machine replacement problem over a span of n years. At the start of each year, we decide whether to keep the machine in service an extra year or to replace it with a new one. Let r(t), c(t), and s(t) represent the yearly revenue, operating cost, and salvage value of a t-year-old machine. The cost of acquir-ing a new machine in any year is 1.

The elements of the DP model are

1.     Stage i is represented by year i, i = 1,2, ... , n.

2.     The alternatives at stage (year) i call for either keeping or replacing the machine at the start of year i.

3.     The state at stage i is the age of the machine at the start of year i.

Given that the machine is t years old at the start of year i, define

Example 10.3-3

A company needs to determine the optimal replacement policy for a current 3-year-old machine over the next 4 years (n = 4). The company requires that a 6-year-old machine be replaced. The cost of a new machine is $100,000. The following table gives the data of the problem.

The determination of the feasible values for the age of the machine at each stage is some-what tricky. Figure 10.6 summarizes the network representing the problem. At the start of year 1, we have a 3-year-old machine. We can either replace it (R) or keep it (K) for another year. At the start of year 2, if replacement occurs, the new machine will be 1 year old; otherwise, the old machine will be 4 years old. The same logic applies at the start of years 2 to 4. If a l-year-old machine is replaced at the start of year 2,3, or 4, its replacement will be 1 year old at the start of the following year. Also, at the start of year 4, a 6-year-old machine must be replaced, and at the end of year 4 (end of the planning horizon), we salvage (5) the machines.

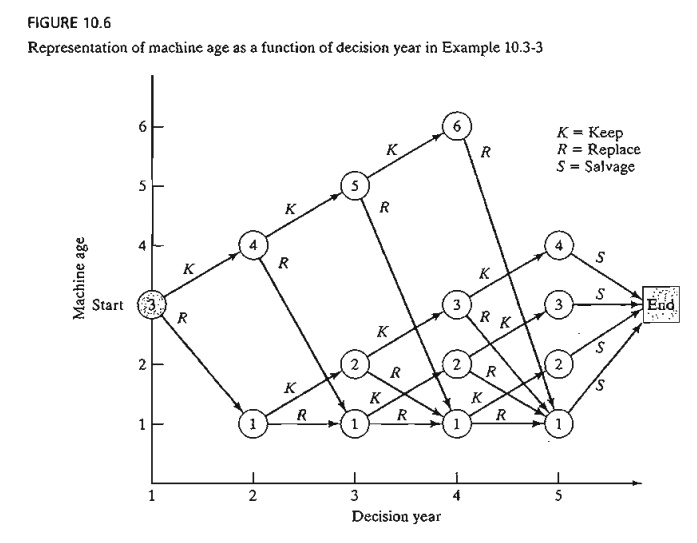
The network shows that at the start of year 2, the possible ages of the machine are 1 and 4 years. For the start of year 3, the possible ages are 1,2, and 5 years, and for the start of year 4, the possible ages are 1,2,3, and 6 years. .

The solution of the network in Figure 10.6 is equivalent to finding the longest route (i.e., maximum revenue) from the start of year 1 to the end of year 4. We will use the tabular form to solve the problem. All values are in thousands of dollars. Note that if a machine is replaced in year 4 (i.e., end of the planning horizon), its revenue will include the salvage value, set), of the replaced machine and the salvage value, s( 1), of the replacement machine.

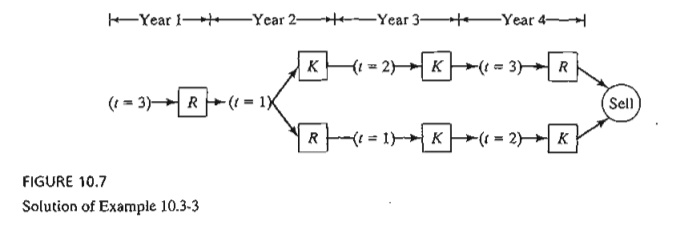
Figure 10.7 summarizes the optimal solution. At the start of year 1, given t = 3, the optimal decision is to replace the machine. Thus, the new machine will be 1 year old at the start of year 2, and l = 1 at the start of year 2 calls for either keeping or replacing the machine. If it is replaced, the new machine will be 1 year old at the start of year 3; otherwise, the kept machine will be 2 years old. The process is continued in this manner until year 4 is reached.

The alternative optimal policies starting in year 1 are (R, K, K, R) and (R, R, K, K). The total cost is $55,300.

PROBLEM SET 10.3C

1. In each of the following cases, develop the network, and find the optimal solution for the model in Example 10.3-3:

a.       The machine is 2 years old at the start of year l.

b.      The machine is 1 year old at the start of year l.

c.       The machine is bought new at the start of year l.

*2. My son, age 13, has a lawn-mowing business with 10 customers. For each customer, he cuts the grass 3 times a year, which earns him $50 for each mowing. He has just paid $200 for a new mower. The maintenance and operating cost of the mower is $120 for the first year in service, and increases by 20% a year thereafter. A l-year-old mower has a resale value of $150, which decreases by 10% a year thereafter. My son, who plans to keep his business until he is 16, thinks that it is more economical to buy a new mower every 2 years. He bases his decision on the fact that the price of a new mower will increase only by 10% a year. Is his decision justified?

3. Circle Farms wants to develop a replacement policy for its 2-year-old tractor over the next 5 years. A tractor must be kept in service for at least 3 years, but must be disposed of after 5 years. The current purchase price of a tractor is $40,000 and increases by 10% a year. The salvage value of a l-year-old tractor is $30,000 and decreases by 10% a year. The current annual operating cost of the tractor is $1300 but is expected to increase by 10% a year.

a)      Formulate the problem as a shortest-route problem.

b)      Develop the associated recursive equation.

c)      Detennine the optimal replacement policy of the tractor over the next 5 years.