Integers

CHAPTER  2

INTEGERS

Learning Objectives

* To understand the necessity for extension of whole numbers to negative numbers.

* To know that the collection of zero, positive and negative numbers forms integers.

* To represent integers on the number line.

* To compare and arrange integers in ascending and descending order.

Introduction

We already have learnt about natural numbers, whole numbers and their properties which were dealt in the first term. Now we shall know about another set of numbers.

Think about the situation

The teacher sees that Yuvan and Subha are ready to play a game with a deck of playing cards. Two different coloured tokens (blue and yellow here) are taken so that they represent the position on a number strip which is numbered from 0 to 20 with 0 as the starting point and which can be extended further.

Consider the cards A, J, Q, K and cards from 2 to 10. Here, let A, J, Q and K denote the numbers 1,11,12 and 13 respectively. We have two designs ♠ ♣ in black colour and two designs ♥ ♦ in red colour inside a deck of cards. Let the joker card represent 0.

Rules for the game

i) If a black card is picked, the player should move the token forward and if a red card is picked, the player should move the token backward as per the number shown on the card.

ii) Whoever reaches the number 20 first will be declared as the winner. (more students can play this game by choosing different coloured tokens)

Observe the following conversation

Yuvan: Subha, I have chosen the blue token.

Subha: Okay, Then I shall take the yellow token.

Yuvan: The number strip is ready as shown below and let both the tokens be placed at the starting position 0. Shall we start playing?

Subha: Yes. I shall pick a card first. I have picked a black card and it shows 5.

 So I will move forward to keep my yellow token at 5 on the number strip.

Yuvan:  Now, I pick …It is black card again and it shows A on it. I will keep my blue token by moving one step forward at 1 on the number strip.

Subha: I pick a red card now and it shows 2 on it.

I need to move backward by 2 steps and I shall keep my token at 3. Is it correct, Yuvan?

Yuvan: Fine Subha. Now, I too have picked the red card and it shows A again. Oh, no..! I will move backward by one step to be again at the starting position 0.

Subha: I am 3 steps ahead of you! Now, I have the red card showing 4 on it. I need to move 4 places backward from 3. But, where shall I keep my token, Yuvan? I moved 3 places only but need one more place behind 0. There is no number on the left of 0.

Subha: Shall I mark it as 1 again?

Yuvan: No, Subha. That won’t be correct. We know that 1 already exists to the right of 0.

Subha: Then, what should I do? I can’t move to the left of '0'. Is the game over or shall I pick another card to continue?

The Teacher intervenes …

Teacher: Yuvan and Subha, why can't you think of extending the number strip to the left of 0 as * 1, * 2 ,*3 and so on such that the distance between *1 and 0 is the same as the distance between 0 and 1 and also the distance between *2 and 0 is the same as the distance between 0 and 2 and extending likewise?

Subha: Yes Teacher, I understand that the * will now indicate that the numbers are on the left of 0, and also the numbers are less than 0.

Teacher: To sustain the interest in the game, continue playing with a small addition in the rule as whoever reaches *20 first, will also be considered as the winner!

Yuvan: So Subha, you shall keep it at *1.

Yuvan: What, if you pick the red card again which shows 4 ?

Subha: I am clear Yuvan. I will move backward 4 places from *1 to keep my token at *5.

Yuvan: Well said…! What can you say, assuming that I am at 5?

Subha: Yes, Yuvan. We will be at the same distance but on the opposite sides of '0'. Am I right?

Yuvan: Yes. you are right but your value is less than mine as you go to the left of '0'.

Think

Who will win finally? Which is the factor that will decide the winner? How far can you extend the numbers on both sides of the strip?

From the above game, we understand that there is a need to go beyond 0 on to its left! We also observe that as 1 is to the right of 0, there should exist *1 to its left with the same distance as 1 and it extends on both sides in the same way.

We generalise this * symbol to ‘–’ (minus or negative sign) to denote the numbers less than '0' which conveys the meaning as less, deficit, reduce, down, left, etc.,

MATHEMATICS ALIVE – INTEGERS IN REAL LIFE

Mariana Snailfishes live in the Mariana Trench at 26,200 feet below the sea level.

Temperature in the Ladakh region of India records at 14°C below 0°C on an average in the month of January every year.

We know that when zero is included to the set of natural numbers then the set of numbers is called as Whole numbers.

Now, let us recall the number line which shows the representation of whole numbers.

We have seen the need to extend the number line beyond 0 to its left. We call the numbers –1, –2, –3, … (to the left of zero) as negative numbers or negative integers and the numbers 1, 2, 3,… (to the right of zero) as positive numbers or positive integers. Hence, the new set of numbers …, -3, -2, -1, 0, 1, 2, 3,… are called Integers. It is denoted by the letter ‘Z’. The Integers are shown in the number line below.

The 'plus' and 'minus' sign before a number tells, on which side the number is placed from zero. ‘–’ symbol in front of a number is read as 'negative' or 'minus'. For example, –5 is read as negative 5 or minus 5.

Note

● The number line can be shown both in horizontal and vertical directions.

● The number 0 is neither positive nor negative and hence has no sign.

● Natural numbers are also called as positive integers and Whole numbers are also called as non-negative integers.

● The positive and the negative numbers together are called as Signed numbers. They are also called as Directed numbers.

● A number without a sign is considered as a positive number. For example, 5 is considered as +5.

DO YOU KNOW?

The letter ‘Z’ was first used by the Germans, because the word for Integers in the German language is “Zahlen” which means “number”.

Example 1

 Draw a number line and mark the integers 6, –5, –1, 4 and –7 on it.

Solution

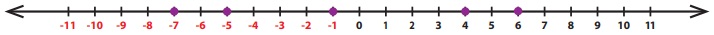
Try these

1 Read the following numbers orally. Try these

 i) +24

ii) –13

 iii) –9

 iv) 8

i) + 24 Positive number 24

ii) −13 negative number 13

iii) − 9 negative number 9

iv) 8 positive number 8

2 Draw a number line and mark the following integers.

 i) 0

 ii) – 6

iii) 5

 iv) – 8

3 Are all natural numbers integers?

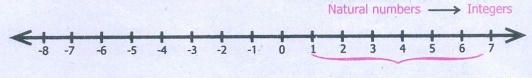
4 Which part of the integers are not whole numbers?

5 How many units should you move to the left of 3 to reach – 4?

More situations on Integers

Activity

Ask your parents / grandparents about the depth at which the various types of vegetables (seeds) should be planted, for their better and efficient growth. For the same, draw a number line indicating the depth of various vegetable seeds. (Draw the planting chart!).