Ordering of Integers

Ordering of Integers

We have already seen the ordering of numbers in the set of natural and whole numbers.

The ordering is possible for integers also.

1. Predecessor and Successor of an Integer

Recall that for a given number its predecessor is one less than it and its successor is one more than it. This applies for integers also.

Example 5

Find the predecessor and successor of i) 0 and ii) −8 on a number line.

Solution

Place the given numbers on the number line then move one unit to their right and left to get the successor and the predecessor respectively.

We can see that the successor of 0 is +1 and the predecessor of 0 is −1 and the successor of −8 is −7 and the predecessor of −8 is −9.

Note

● Every positive integer is greater than each of the negative integers. Example: 3 > −5

● 0 is less than every positive integer but greater than every negative integer. Example: 0<2 but 0> −2

2. Comparing Integers

Ordering of integers is to compare them. It is very easy to compare and order integers by using a number line.

When we move towards the right of a number on the number line, the numbers become larger. On the other hand, when we move towards the left of a number on the number line, the numbers become smaller.

We know that 4 < 6, 8 > 5 and so on. Now let us consider two integers say −4 and 2.

Mark them on the number line as shown below.

Fix −4 now. See whether 2 is to the right or the left of −4. In this case, 2 is to the right of−4 and in the positive direction. So, 2 > −4 or otherwise −4 < 2.

Example 6

Compare −14 and −11

Solution

Draw number line and plot the numbers −14 and −11 as follows.

Fixing −11, we find −14 is to the left of −11. So, −14 is smaller than −11. That is, −14 < −11.

Think

For two numbers, say 3 and 5, we know that 5 > 3. Will there be a change in the inequality if both the numbers have negative sign before them?

Activity

Take two cards from a deck of playing cards and identify, which is greater between them, assuming that the Joker card represents zero, black cards represent positive integers, red cards represent negative integers and the cards A, J, Q and K represent 1,11,12 and 13 respectively.

Example 7

Arrange the following integers in ascending order:

−15, 0, −7, 12, 3, −5, 1, −20, 25, 18

Solution

Step 1: First, separate the positive integers as 12, 3, 1, 25, 18 and the negative integers as −15, −7, −5, −20

Step 2: We can easily arrange positive integers in ascending order as 1, 3, 12, 18, 25 and negative integers in ascending order as −20, −15, −7, −5.

Step 3: As 0 is neither positive nor negative, it stays at the middle and now the arrangement −20, −15, −7, −5, 0, 1, 3, 12, 18 and 25 is in ascending order.

Try these

i) Is −15 < −26? Why?

−15 < −26 is false. When we move towards The right of a number on the number line, the numbers become larger. On the other hand, when we move towards the left of a number on the number line, the numbers become smaller.

−26 is left of −15. So − 26 is less than −15

−26 < −15 

ii) Which is smaller −3 or −5? Why?

−5 < −3

In the number line −5 is left of −3. So −5 is less than −3.

iii) Which is greater 7 or −4? Why?

7 > −4.

In the number line 7 is right of −4

So 7 is greater than −4.

iv) Which is the greatest negative integer?

The greatest negative integer −1

v) Which is the smallest positive integer?

The smallest positive integer +1

ICT CORNER

Integers

Expected Outcome

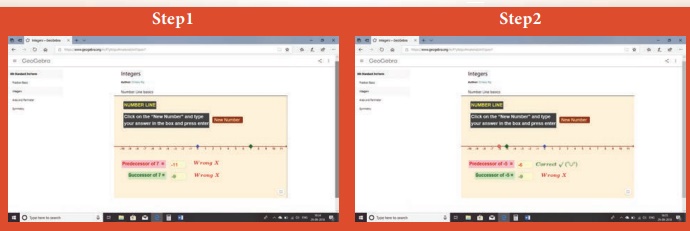
Step 1

Open the Browser by typing the URL Link given below (or) Scan the QR Code. GeoGebra work sheet named “Integers” will open. There is a worksheet under the title Number Line basics.

Step 2

Click on the “New Number” to get new question and type your answer in the respective check boxes, next to Predecessor and Successor and press enter..

Browse in the link:

Integers: https://ggbm.at/mt7qxxn7 or Scan the QR Code.