Infrared Spectrophotometry: Theory

THEORY

The underlying principle of infrared spectroscopy is based upon the molecular vibrations which is further composed of the stretching and the bending vibrations of a molecule.

Therefore, it would be necessary to have a clear concept of various modes of vibrations often encoun-tered in different molecules having a variety of functional moieties, laws governing them and the mathemati-cal derivations related to them.

1. MOLECULAR VIBRATIONS

A molecule may not be looked upon as a rigid assemblage of atoms. Rather it may be regarded as a sort of flexible system comprising of balls of varying masses representing the atoms of a molecule and springs of varying strengths representing the chemical bonds of a molecule.

The vibrations for molecules are of two types, namely :

(a) Stretching, and

(b) Bending (or deformation).

1.1.  Stretching

Vibration causes stretching whereby the distance between the two atoms increases or decreases, but the atoms remain in the same bond axis.

1.2. Bending (or Deformation)

Vibration causes bending whereby the position of the atom changes relative to the original bond axis.

Therefore, the various stretching and bending vibrations of a bond usually take place at particular quantized frequencies. Thus, in a situation where upon the infrared light having the same frequency is inci-dent on the molecule, energy is absorbed, and the net effect could be observed by an increase in the ampli-tude of that vibration. In another situation, whereby the molecule reverts from the excited state to the ground state, the absorbed energy is released in the form of heat.

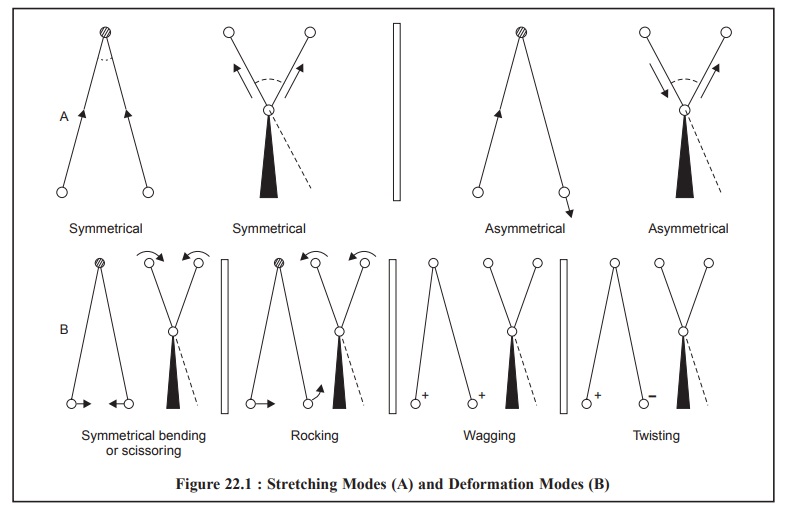
The various stretching and bending vibrations that can exist within a molecule may be represented schematically as shown below in Figure 22.1 :

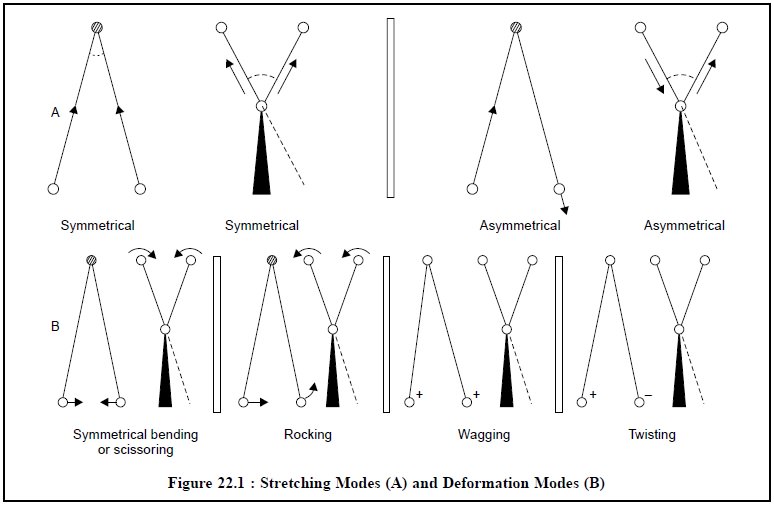
There are two types of Bending (or deformation) Modes, namely :

(i) Below the plane of paper and perpendicular to it designated by (+) sign, and

(ii) Above the plane of paper and perpendicular to it represented by (–) sign.

1.3. Stretching Vibrations

In this particular instance, the atoms move invariably along the bond that joins them e.g., C—H ; C = O ; O—H ; N—H.

The stretching vibrations may be further sub-divided into two categories, namely :

(a) Symmetrical Stretching : In this case, the two hydrogen atoms either move towards or away from the central carbon atom in unison, thereby either altering the interatomic distance or causing no change in valence angle (Figure 22.1).

(b) Asymmetrical Stretching : In this instance, one hydrogen atom approaches the carbon atom while the other moves away from the carbon atom (Figure 22.1).

1.4. Bending (or Deformation) Vibrations

In the event when a three-atom system forms part of a larger molecule, it is quite possible to have bending (or deformation) vibrations which essentially involve oscillation of the atoms, or group as a whole and is perpendicular to its chemical bond (Figure 22.1).

Such bending vibrations can take place either in-plane or out-of-plane.

1.4.1. In-Plane Bending Vibrations

These are two types :

(a) Scissoring or Symmetrical Bending : In this case, the two atoms connected to a central atom either move toward or away from each other with certain deformation of the valence angle.

(b) Rocking : In this case, the structural unit swings back and forth in the plane of the molecule.

1.4.2. Out-of Plane Bending Vibrations

These are also of two kinds, namely :

(a) Wagging : In this case the structural unit swings back and forth out of the plane of the molecule.

(b) Twisting : In this case the structural unit rotates about the bond that joins it to the rest of the molecule.

1.4.3. Explanations of Bending and Stretching Vibrations

The bending (or deformation) vibrations generally require less energy and take place at longer-wave-length than the corresponding stretching vibrations.

In contrast, the stretching vibrations are observed to occur with respect to their corresponding bond-strengths.

Examples : The typical examples of triple-bond, double-bond and single-bond are given below :

Whenever a very small proton like : C—H ; O—H ; or N—H is involved in a single bond, the stretch-ing vibrations normally take place at much higher frequency i.e., 3700-2630 cm^–1 (or 2.7-3.8 µ). It is, how-ever, interesting to note that O—H bond absorbs at 2.8 µ (or 3570 cm^–1), whereas O—D bond absorbs at 3.8μ (or 2630 cm^–1). In this specific case, the strengths of the two bonds are more or less the same, but the mass of one atom is almost doubled.

1.4.4. Calculation of Vibrational Frequencies

The vibrational frequency may be calculated with fairly remarkable accuracy by the help of Hooke’s Law and is expressed as :

         ...............................(a)

Where , ν = Frequency,

k = Force constant of the bond, and

m₁ and m₂ = Masses of two atoms.

The quantity m₁m₂/(m₁ + m₂) is often expressed as µ, the reduced mass of the system.

Example : Calculate the approximate frequency of the C—H stretching vibration from the following dara:

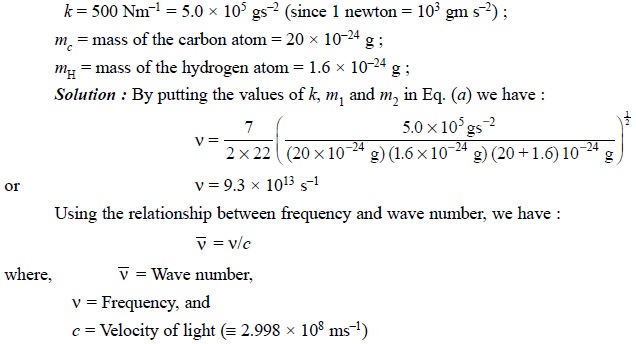
Therefore, we have :

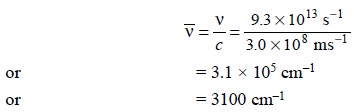
However, it is pertinent to restate the underlying principles embodied in these calculations, that is “the vibrational frequency of a bond is expected to increase when the bond strength increases, and also when the reduced mass of the system decreases”.

1.5. Salient Features of IR-Spectroscopy

There are, in fact, three vital points that may be noted with regard to IR-spectroscopy, namely :

(a) Most intense peaks in the IR-spectrum are solely due to absorption peaks caused by the stretching vibrations,

(b) Molar extinction coefficient in IR-spectroscopy varies from 0-2000 cm^–1, and

(c) Molar extinction coefficient is directly proportional to the square of the change in the dipole moment* of the molecule that the particular vibration affords.

2. FACTORS INFLUENCING VIBRATIONAL FREQUENCIES

There are a number of factors that influence the precise frequency of a molecular vibration, namely :

(a) Vibrational coupling,

(b) Hydrogen bonding,

(c) Electronic Effects, and

(d) Field Effects.

All the above factors shall be discussed briefly with appropriate examples and explanations, wherever necessary, below :

2.1. Vibrational Coupling

The following four vibrations may be observed in the high-resolution spectra of compounds contain-ing both —CH₂ and —CH₃ groups.

C—H            :  One stretching frequency,

Examples : The three typical examples are described below, namely :

(a) Carboxylic Acid Anhydrides : For instance :

Following are the salient features :

·              It affords two C = O stretching absorptions viz., ν_anti and ν_symm between frequency 1800-1900 cm^–1 having a separation of about 65 cm^–1 ;

·              The coupling solely occurs between the two carbonyl groups, that are indirectly linked through —O— ;

·              Resonance : The interaction is probably encouraged due to the single as well as double-bond character prevailing in the carbonyl-oxygen bonds brought about by resonance as shown below :

(b) Amides 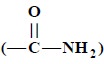 : The functional moiety ‘amide’ shows two distinct bands around 1600- 1700 cm^–1 caused due to C = O str. and N—H def. These bands are also known as Amide-I and Amide-II bands.

Amide-I :        is formed due to C = O str. and amounts to a level as high as 80% ;

Amide-II : is a strongly coupled interaction between N—H def. and C—N str. and accounts for the remaining 20%.

(c) Aldehydes 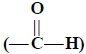 : The functional group ‘aldehyde’ offers C—H str. absorption band which appears as a doublet because of interaction between the two components, namely : C—H str. fundamental and C—H def. overtone.

2.2. Hydrogen Bonding

In general, the hydrogen bonding present in O—H and N—H compounds give rise to a number of effects in the IR-spectra. However, the carbonyl groups or aromatic rings present in the same molecule as the O—H or N—H group may cause similar shifts by intramolecular action.

A few typical examples involving hydrogen bonding in a wide-range of organic compounds are discussed below :

(a) Alcohols and Phenols : Interestingly, alcohols and phenols, in condensed phases (KBr-Disc/ liquid film), are strongly hydrogen-bonded thereby forming dimers, trimers and tetramers that ultimately leads to a wide envelope of absorptions thus causing broadening of the absorption band.

In diluted solution and in an inert solvent (e.g., 1-butanol 1% in CCl₄) the proportion of free molecules enhances that gives rise to the 3650 cm^–1 band.

Another school of thought suggests that the hydrogen-bond may be regarded as a resonance hy-brid I and II (approximating overall to III)-thereby the original O—H bond undergoes a lengthen-ing as depicted below :

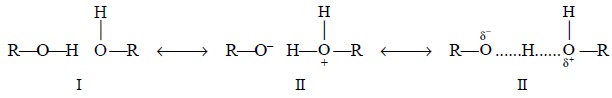
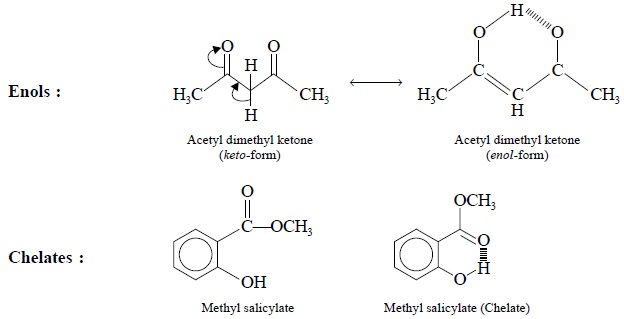
(b) Enols and Chelates : The hydrogen-bonding existing in enols and chelates is found to be specifi-cally strong and the observed O—H str. frequencies may be very low (2800 cm^–1). In this particu-lar instance, the dilution by an inert solvent (e.g., 1-butanol 1% in CCl₄) cannot even break these bonds, therefore, free O—H str. may not be observed at low concentrations.

The above observations may be explained by citing the example of acetyl dimethyl ketone (for enols) and methyl salicylate (for chelates) as shown below :

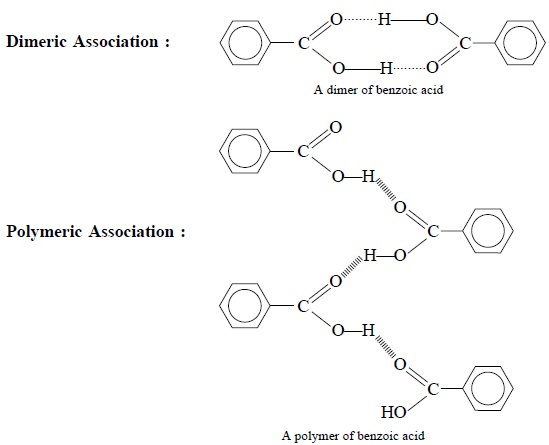
(c) Carboxylic Acids : Let us consider the example of benzoic acid IR-spectrum in KBr-disc wherein we may observe a relatively broad band caused due to hydrogen-bonded O—H str. between 2500-3500 cm^–1. These broad bands are formed due to the dimeric and polymeric associations of benzoic acid as shown below :

(d) π-Cloud Interactions : Since alkene and aromatic π-bonds behave as Lewis bases, they may form hydrogen bonds to acidic hydrogens e.g.,

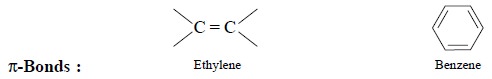
Example : The frequency of O—H str. in phenols is lowered by 40-100 cm^–1 when the IR-spec-trum is recorded in a benzene solution as compared to a carbon tetrachloride solution.

(e) Amines : Amines usually show two distinct bands due to N—H stretching in different environ-ments. In condensed-phase spectra, amines show bonded N—H str. around 3300 cm^–1 and in dilute solution a new band near 3600 cm^–1 corresponding to free N—H str. It may be attributed due to the fact that the electronegativity of nitrogen is less than that of oxygen and hence the hydrogen bonds in amines are weaker than in alcohols.

2.3. Electronic Effects

On the basis of theoretical principles one may explain the frequency shifts that normally take place in molecular vibrations when the substituents are altered :

A few such classical examples are enumerated with appropriate explanations.

(a) Conjugation Effect : It is observed to lower the frequency of both C = C str. and C = O str., irrespective of the fact it is brought about by either αβ-unsaturation or by an aromatic ring as shown below :

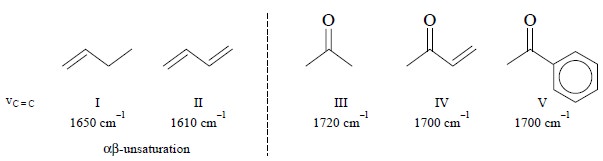
Explanation : In II, lowering of band order in the C = C bond is observed due to conjugation effect whereby the stretching vibration frequency is decreased by 40-50 cm^–1 (compare I and II above). In a similar manner, in V delocalization of π-electrons between C = O and the benzene ring enhances the double-bond character of the bond joining the C = O to the ring. It ultimately leads to a lower band order in the C = O bond thereby decreasing the stretching vibration fre-quency by 20-30 cm^–1 (compare III and V above).

(b) Mesomeric (or Resonance) Effect : Whenever a molecule can be represented by two or more structures that differ only in the arrangement of electrons—that is, by structures that have the same arrangement of atomic nuclei-there is resonance.

It may be further expatiated with the help of the following typical examples :

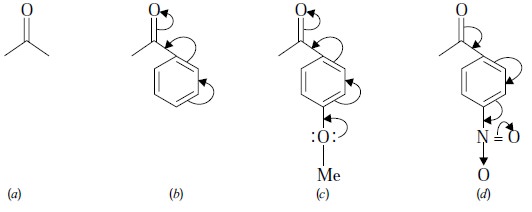
—OMe : Electron Releasing Moiety

—NO₂ : Electron Withdrawing Moiety

In (b) above, the presence of a phenyl ring increases the mesomeric shift thereby lowering C = O str. frequency.

+M Group : viz., p-OMe (an electron releasing function)—its presence as depicted in (c) above will further lower frequencies due to enhanced mesomeric effect.

– M Group : viz., p-NO₂ (an electron withdrawing function)—its presence as shown in (d) above will further increase frequencies due to decreased mesomeric effect.

(c) Inductive Effects : The inductive effects solely depends upon the ‘intrinsic’ tendency of a substituent to either release or withdraw electrons-by definition, its electronegativity acting either through the molecular chain or through space. This effect usually weakens steadily with increas-ing distance from the substituent.

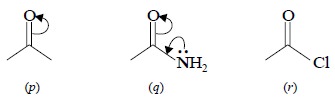
The ‘inductive effects’ shall now be discussed specifically with regard to the various functional moieties such as : amides, acyl chlorides, alkyl esters and aryl esters :

(i) Amides : (q), The + M effect causes weakening of the C = O bond, leading to the corresponding ketone (p). In this particular instance, the – I effect of nitrogen is being dominated by + M effect.

(ii) Acyl Chlorides : (r), the – I effect of Cl is more effective than + M effect, thereby causing an opposite shift (to higher frequency).

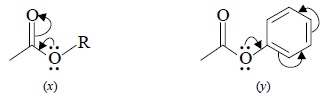
(iii) Alkyl Esters : (x), it has been observed that a conflict between I and M effects invariably takes place in the case of esters. Here, the non-bonding electrons residing on oxygen enhance the + M conjugation thereby decreasing the C = O frequency.

(iv) Aryl Esters : (y), here the non-bonding electrons located on oxygen are partially drawn into the benzene ring and thereafter their conjugation with C = O is minimised. The net effect would be that – I effect of oxygen becomes dominant and consequently C = O moves to a higher frequency.

(d) Field Effects : It has been observed that two functional groups often influence each other’s vibra-tional frequencies by a through-space interaction that may be either steric and/or electrostatic in nature.

A typical example of ortho-chlorobenzoic acid esters is shown below :

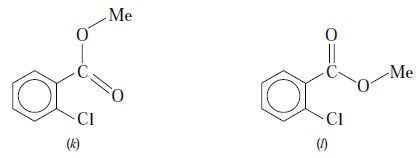
In the above instance, the field effect shifts the C = O frequency in the rotational isomer (k) and not in the isomer (1). As both isomers are usually found to be present together, therefore, two C = O str. absorptions are observed in the spectrum of this compound.

The various aspects discussed above in Sections, give a sufficient in-depth knowledge of theoretical considerations related to the better understanding of infrared spectroscopy.