Inference

Inference

Inference is a way to infer or derive sensitive data from nonsensitive data. The inference problem is a subtle vulnerability in database security.

The database in Table 6 -7 can help illustrate the inference problem. Recall that AID is the amount of financial aid a student is receiving. FINES is the amount of parking fines still owed. DRUGS is the result of a drug-use survey: 0 means never used and 3 means frequent user. Obviously this information should be kept confidential. We assume that AID, FINES, and DRUGS are sensitive fields, although only when the values are related to a specific individual. In this section, we look at ways to determine sensitive data values from the database.

Direct Attack

In a direct attack, a user tries to determine values of sensitive fields by seeking them directly with queries that yield few records. The most successful technique is to form a query so specific that it matches exactly one data item.

In Table 6-7, a sensitive query might be

This query discloses that for record ADAMS, DRUGS=1. However, it is an obvious attack because it selects people for whom DRUGS=1, and the DBMS might reject the query because it selects records for a specific value of the sensitive attribute DRUGS.

A less obvious query is

List NAME where

 (SEX=M DRUGS=1)

(SEX M SEX F)

(DORM=AYRES)

On the surface, this query looks as if it should conceal drug usage by selecting other non-drug-related records as well. However, this query still retrieves only one record, revealing a name that corresponds to the sensitive DRUG value. The DBMS needs to know that SEX has only two possible values so that the second clause will select no records. Even if that were possible, the DBMS would also need to know that no records exist with DORM=AYRES, even though AYRES might in fact be an acceptable value for DORM.

Organizations that publish personal statistical data, such as the U.S. Census Bureau, do not reveal results when a small number of people make up a large proportion of a category. The rule of "n items over k percent" means that data should be withheld if n items represent over k percent of the result reported. In the previous case, the one person selected represents 100 percent of the data reported, so there would be no ambiguity about which person matches the query.

Indirect Attack

Another procedure, used by the U.S. Census Bureau and other organizations that gather sensitive data, is to release only statistics. The organizations suppress individual names, addresses, or other characteristics by which a single individual can be recognized. Only neutral statistics, such as sum, count, and mean, are released.

The indirect attack seeks to infer a final result based on one or more intermediate statistical results. But this approach requires work outside the database itself. In particular, a statistical attack seeks to use some apparently anonymous statistical measure to infer individual data. In the following sections, we present several examples of indirect attacks on databases that report statistics.

Sum

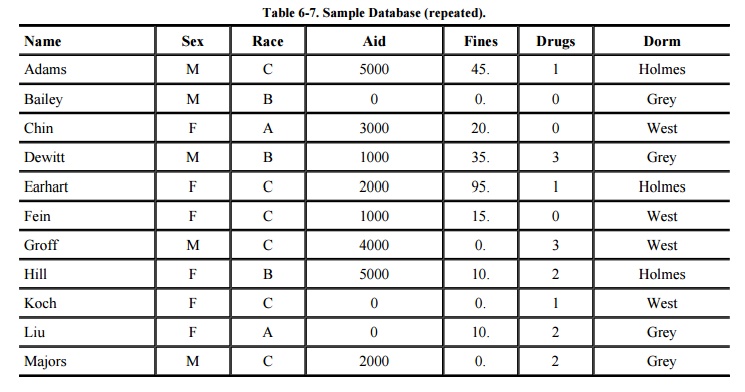
An attack by sum tries to infer a value from a reported sum. For example, with the sample database in Table 6-7, it might seem safe to report student aid total by sex and dorm. Such a report is shown in Table 6-8. This seemingly innocent report reveals that no female living in Grey is receiving financial aid. Thus, we can infer that any female living in Grey (such as Liu) is certainly not receiving financial aid. This approach often allows us to determine a negative result.

Count

The count can be combined with the sum to produce some even more revealing results. Often these two statistics are released for a database to allow users to determine average values. (Conversely, if count and mean are released, sum can be deduced.)

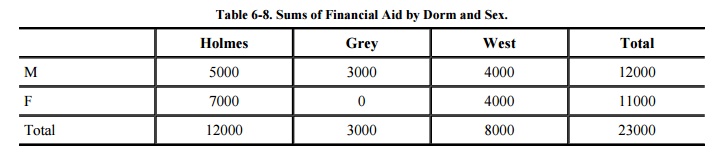
Table 6-9 shows the count of records for students by dorm and sex. This table is innocuous by itself. Combined with the sum table, however, this table demonstrates that the two males in Holmes and West are receiving financial aid in the amount of $5000 and $4000, respectively. We can obtain the names by selecting the subschema of NAME, DORM, which is not sensitive because it delivers only low-security data on the entire database.

Mean

The arithmetic mean (average) allows exact disclosure if the attacker can manipulate the subject population. As a trivial example, consider salary. Given the number of employees, the mean salary for a company and the mean salary of all employees except the president, it is easy to compute the president's salary.

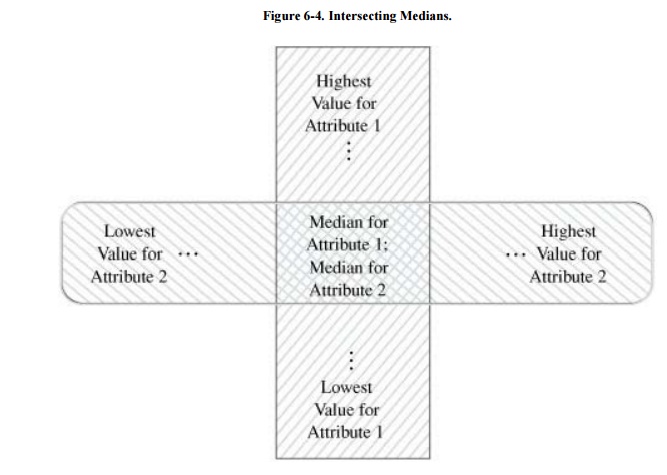
Median

By a slightly more complicated process, we can determine an individual value from medians. The attack requires finding selections having one point of intersection that happens to be exactly in the middle, as shown in Figure 6-4.

For example, in our sample database, there are five males and three persons whose drug use value is 2. Arranged in order of aid, these lists are shown in Table 6-10. Notice that Majors is the only name common to both lists, and conveniently that name is in the middle of each list. Someone working at the Health Clinic might be able to find out that Majors is a white male whose drug-use score is 2. That information identifies Majors as the intersection of these two lists and pinpoints Majors' financial aid as $2000. In this example, the queries

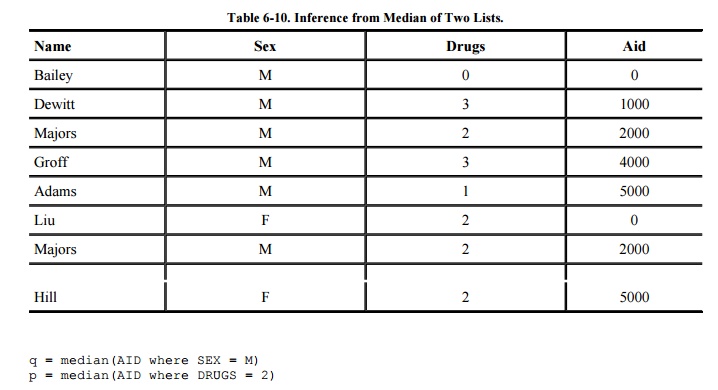
reveal the exact financial aid amount for Majors.

Tracker Attacks

As already explained, database management systems may conceal data when a small number of entries make up a large proportion of the data revealed. A tracker attack can fool the database manager into locating the desired data by using additional queries that produce small results. The tracker adds additional records to be retrieved for two different queries; the two sets of records cancel each other out, leaving only the statistic or data desired. The approach is to use intelligent padding of two queries. In other words, instead of trying to identify a unique value, we request n - 1 other values (where there are n values in the database). Given n and n - 1, we can easily compute the desired single element.

Controls for Statistical Inference Attacks

Denning and Schlörer [DEN83a] present a very good survey of techniques for maintaining security in databases. The controls for all statistical attacks are similar. Essentially, there are two ways to protect against inference attacks: Either controls are applied to the queries or controls are applied to individual items within the database. As we have seen, it is difficult to determine whether a given query discloses sensitive data. Thus, query controls are effective primarily against direct attacks.

Suppression and concealing are two controls applied to data items. With suppression, sensitive data values are not provided; the query is rejected without response. With concealing, the answer provided is close to but not exactly the actual value.

These two controls reflect the contrast between security and precision. With suppression, any results provided are correct, yet many responses must be withheld to maintain security. With concealing, more results can be provided, but the precision of the results is lower. The choice between suppression and concealing depends on the context of the database. Examples of suppression and concealing follow.

Limited Response Suppression

The n-item k-percent rule eliminates certain low-frequency elements from being displayed. It is not sufficient to delete them, however, if their values can also be inferred. To see why, consider Table 6-11, which shows counts of students by dorm and sex.

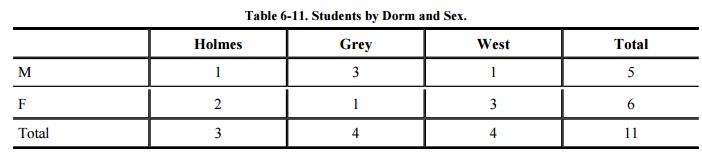
The data in this table suggest that the cells with counts of 1 should be suppressed; their counts are too revealing. But it does no good to suppress the MaleHolmes cell when the value 1 can be determined by subtracting FemaleHolmes (2) from the total (3) to determine 1, as shown in Table 6-12.

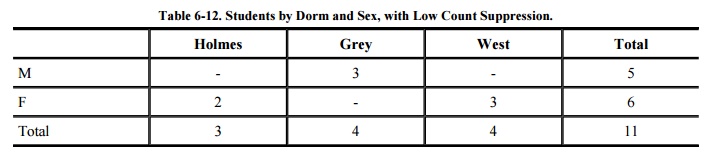
When one cell is suppressed in a table with totals for rows and columns, it is necessary to suppress at least one additional cell on the row and one on the column to provide some confusion. Using this logic, all cells (except totals) would have to be suppressed in this small sample table. When totals are not provided, single cells in a row or column can be suppressed.

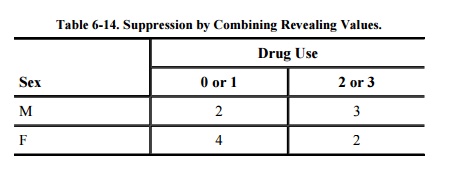
Combined Results

Another control combines rows or columns to protect sensitive values. For example, Table 6-13 shows several sensitive results that identify single individuals. (Even though these counts may not seem sensitive, they can be used to infer sensitive data such as NAME; therefore, we consider them to be sensitive.)

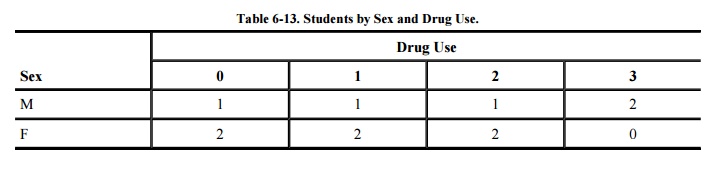
These counts, combined with other results such as sum, permit us to infer individual drug-use values for the three males, as well as to infer that no female was rated 3 for drug use. To suppress such sensitive information, it is possible to combine the attribute values for 0 and 1, and also for 2 and 3, producing the less sensitive results shown in Table 6-14. In this instance, it is impossible to identify any single value.

Another way of combining results is to present values in ranges. For example, instead of releasing exact financial aid figures, results can be released for the ranges $01999, $20003999, and $ 4000 and above. Even if only one record is represented by a single result, the exact value of that record is not known. Similarly, the highest and lowest financial aid values are concealed.

Yet another method of combining is by rounding. This technique is actually a fairly well-known example of combining by range. If numbers are rounded to the nearest multiple of 10, the effective ranges are 05, 615, 1625, and so on. Actual values are rounded up or down to the nearest multiple of some base.

Random Sample

With random sample control, a result is not derived from the whole database; instead the result is computed on a random sample of the database. The sample chosen is large enough to be valid. Because the sample is not the whole database, a query against this sample will not necessarily match the result for the whole database. Thus, a result of 5 percent for a particular query means that 5 percent of the records chosen for the sample for this query had the desired property. You would expect that approximately 5 percent of the entire database will have the property in question, but the actual percentage may be quite different.

So that averaging attacks from repeated, equivalent queries are prevented, the same sample set should be chosen for equivalent queries. In this way, all equivalent queries will produce the same result, although that result will be only an approximation for the entire database.

Random Data Perturbation

It is sometimes useful to perturb the values of the database by a small error. For each x_i that is the true value of data item i in the database, we can generate a small random error term ε_i and add it to x_i for statistical results. The ε values are both positive and negative, so that some

reported values will be slightly higher than their true values and other reported values will be lower. Statistical measures such as sum and mean will be close but not necessarily exact. Data perturbation is easier to use than random sample selection because it is easier to store all the ε values in order to produce the same result for equivalent queries.

Query Analysis

A more complex form of security uses query analysis. Here, a query and its implications are analyzed to determine whether a result should be provided. As noted earlier, query analysis can be quite difficult. One approach involves maintaining a query history for each user and judging a query in the context of what inferences are possible given previous results.

Conclusion on the Inference Problem

There are no perfect solutions to the inference problem. The approaches to controlling it follow the three paths listed below. The first two methods can be used either to limit queries accepted or to limit data provided in response to a query. The last method applies only to data released.

Suppress obviously sensitive information. This action can be taken fairly easily. The tendency is to err on the side of suppression, thereby restricting the usefulness of the database.

Track what the user knows. Although possibly leading to the greatest safe disclosure, this approach is extremely costly. Information must be maintained on all users, even though most are not trying to obtain sensitive data. Moreover, this approach seldom takes into account what any two people may know together and cannot address what a single user can accomplish by using multiple IDs.

Disguise the data. Random perturbation and rounding can inhibit statistical attacks that depend on exact values for logical and algebraic manipulation. The users of the database receive slightly incorrect or possibly inconsistent results.

It is unlikely that research will reveal a simple, easy-to-apply measure that determines exactly which data can be revealed without compromising sensitive data.

Nevertheless, an effective control for the inference problem is just knowing that it exists. As with other problems in security, recognition of the problem leads to understanding of the purposes of controlling the problem and to sensitivity to the potential difficulties caused by the problem. However, just knowing of possible database attacks does not necessarily mean people will protect against those attacks, as explained in Sidebar 6-4. It is also noteworthy that much of the research on database inference was done in the early 1980s, but this proposal appeared almost two decades later.

Aggregation

Related to the inference problem is aggregation, which means building sensitive results from less sensitive inputs. We saw earlier that knowing either the latitude or longitude of a gold mine does you no good. But if you know both latitude and longitude, you can pinpoint the mine. For a more realistic example, consider how police use aggregation frequently in solving crimes: They determine who had a motive for committing the crime, when the crime was committed, who had alibis covering that time, who had the skills, and so forth. Typically, you think of police investigation as starting with the entire population and narrowing the analysis to a single person. But if the police officers work in parallel, one may have a list of possible suspects, another may have a list with possible motive, and another may have a list of capable persons. When the intersection of these lists is a single person, the police have their prime suspect.

Addressing the aggregation problem is difficult because it requires the database management system to track which results each user had already received and conceal any result that would let the user derive a more sensitive result. Aggregation is especially difficult to counter because it can take place outside the system. For example, suppose the security policy is that anyone can have either the latitude or longitude of the mine, but not both. Nothing prevents you from getting one, your friend from getting the other, and the two of you talking to each other.

Recent interest in data mining has raised concern again about aggregation. Data mining is the process of sifting through multiple databases and correlating multiple data elements to find useful information. Marketing companies use data mining extensively to find consumers likely to buy a product. As Sidebar 6-5 points out, it is not only marketers who are interested in aggregation through data mining.

Sidebar 6-4: Iceland Protects Privacy Against Inference

In 1998, Iceland authorized the building of a database of citizens' medical records, genealogy, and genetic information. Ostensibly, this database would provide data on genetic diseases to researchersmedical professionals and drug companies. Iceland is especially interesting for genetic disease research because the gene pool has remained stable for a long time; few outsiders have moved to Iceland, and few Icelanders have emigrated. For privacy, all identifying names or numbers would be replaced by a unique pseudonym. The Iceland health department asked computer security expert Ross Anderson to analyze the security aspects of this approach.

Anderson found several flaws with the proposed approach [AND98a]:

  Inclusion in the genealogical database complicates the task of maintaining individuals' anonymity because of distinctive family features. Moreover, parts of the genealogical database are already public because information about individuals is published in their birth and death records. It would be rather easy to identify someone in a family of three children born, respectively, in 1910, 1911, and 1929.

  Even a life's history of medical events may identify an individual. Many people would know that a person broke her leg skiing one winter and contracted a skin disease the following summer.

  Even small sample set restrictions on queries would fail to protect against algebraic attacks.

  To analyze the genetic data, which by its nature is necessarily of very fine detail, researchers would require the ability to make complex and specific queries. This same powerful query capability could lead to arbitrary selection of combinations of results.

For these reasons (and others), Anderson recommended against continuing to develop the public database. In spite of these problems, the Iceland Parliament voted to proceed with its construction and public release [JON00].

Aggregation was of interest to database security researchers at the same time as was inference. As we have seen, some approaches to inference have proven useful and are currently being used. But there have been few proposals for countering aggregation.