Important Answers: Deflection of Beams

BEAMS DEFLECTION

1. List any four methods of determining slope and deflection of loaded beam?

i)Double integration method,

ii)Macaulay’s method,

iii)Moment area method and

iv)Conjugate beam method

2. What is the relation between slope, deflection and radius of curvature of a beam?

1/R =(d2y)/(dx2)

 Where R =radius of curvature.

Y= deflection.

3.       State two assumptions made in theEuler’s co

i)The cross section of the column is uniform throughout its length and

ii)The length of the column is very long as compared to its cross sectional dimensions.

4.       State Slenderness ratio

The ratio between actual length to least radius of gyration Slenderness ratio = L / k

5.       Write the equivalent length of column for a column.

          i)One end is fixed and other end is free Effective length L= 2l

          ii)Both ends are fixed Effective length L= l/2      

6.       State   the   limitations   of   Euler’s formula.

If the slenderness ratio is small, the crippling stress will be high. But for the column material, the  crippling stress cannot be greater than the crushing stress. In the limiting case, we can find the value of slenderness ratio for which the crippling stress is equal to the crushing stress.

7.       Describe the double integration method.

          While integrating twice the original differential equation, we will get two constant C1 and C2. The value of these constants may be found by using the end conditions.

8.       Calculate the effective length of a long column, whose actual length is 4m when i)both ends are fixed ii)one end is fixed while the other end is free?

          i)Both ends are fixed Effective length L= l/2 =4/2=2m           

          ii)One end is fixed while the other end is free Effective length L= 2l=2x4=8m

9.       Define column

A structural member which is subjected to axial compressive load is known as column.

10. Define crippling load

The load at which the column just buckles is known as crippling load.

11. Define shear force and bending moment?

SF at any cross section is defined as algebraic sum of the vertical forces acting either side of

beam.

BM at any cross section is defined as algebraic sum of the moments of all the forces which are placed either side from that point.

12. When will bending moment is maximum?

BM will be maximum when shear force change its sign.

13. What is maximum bending moment in a simply supported beam of span ‘L’subjected to UDL of ‘w’over entire span?

Max BM =wL²/8

14. In a simply supported beam how will you locate point of maximum bending moment?

The bending moment is max. when SF is zero. Writing SF equation at that point and equating to zero we can find out the distances ‘x’from one end .then find maximum bending moment at that point by taking moment on right or left hand side of beam.

15. What is shear force and bending moment diagram?

It shows the variation of the shear force and bending moment along the length of the beam.

16.                        What are the types of beams?

1. Cantilever beam

2. Simply supported beam

3. Fixed beam

4. Continuous beam

5. over hanging beam

17.                        What are the types of loads?

1. Concentrated load or point load

2. Uniform distributed load (udl)

3. Uniform varying load(uvl)

18.                        Write the assumptions in the theory of simple bending?

1. The material of the beam is homogeneous and isotropic.

The beam material is stressed within the elastic limit and thus obey hooke’slaw.

3. Each layer of the beam is free to expand or contract independently about the layer, above or

below.

4. The value of E is the same in both compression and tension.

19.                        Write the theory of simple bending equation?

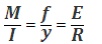
Where,

M - Maximum bending moment I - Moment of inertia

f  - Maximum stress induced

y- Distance from the neutral axis E - Young’smodulus

R –Radius of neutral layer.

20. Define: Neutral Axis

The N.A of any transverse section is defined as the line of intersection of the neutral layer with the transverse section.

21. Define: Moment of resistance

Due to pure bending, the layers above the N.A are subjected to compressive stresses, whereas the layers below the N.A are subjected to tensile stresses. Due to these stresses, the forces will be acting on the layers. These forces will have moment about the N.A. The total moment of these forces about the N.A for a section is known as moment of resistance of the section.

22. Define: Section modulus

Section modulus is defined as the ratio of moment of inertia of a section about the N.A to the distance of the outermost layer from the N.A.

Section modulus,

Where, I –M.O.I about N.A

y_max - Distance of the outermost layer from the N.A