IIR Filter Design

IIR FILTER DESIGN

INTRODUCTION

To remove or to reduce strength of unwanted signal like noise and to improve the quality of required signal filtering process is used. To use the channel full bandwidth we mix up two or more signals on transmission side and on receiver side we would like to separate it out in efficient way.

Hence filters are used. Thus the digital filters are mostly used in

1.        Removal of undesirable noise from the desired signals

2.        Equalization of communication channels

3.        Signal detection in radar, sonar and communication

4.        Performing spectral analysis of signals.

Analog and digital filters

In signal processing, the function of a filter is to remove unwanted parts of the signal, such as random noise, or to extract useful parts of the signal, such as the components lying within a certain frequency range.

The following block diagram illustrates the basic idea.

There are two main kinds of filter, analog and digital. They are quite different in their physical makeup and in how they work.

An analog filter uses analog electronic circuits made up from components such as resistors, capacitors and op amps to produce the required filtering effect. Such filter circuits are widely used in such applications as noise reduction, video signal enhancement, graphic equalizers in hi-fi systems, and many other areas.

In analog filters the signal being filtered is an electrical voltage or current which is the direct analogue of the physical quantity (e.g. a sound or video signal or transducer output) involved.

A digital filter uses a digital processor to perform numerical calculations on sampled values of the signal. The processor may be a general-purpose computer such as a PC, or a specialized DSP (Digital Signal Processor) chip.

The analog input signal must first be sampled and digitized using an ADC (analog to digital converter). The resulting binary numbers, representing successive sampled values of the input signal, are transferred to the processor, which carries out numerical calculations on them. These calculations typically involve multiplying the input values by constants and adding the products together. If necessary, the results of these calculations, which now represent sampled values of the filtered signal, are output through a DAC (digital to analog converter) to convert the signal back to analog form.

In a digital filter, the signal is represented by a sequence of numbers, rather than a voltage or current.

The following diagram shows the basic setup of such a system.

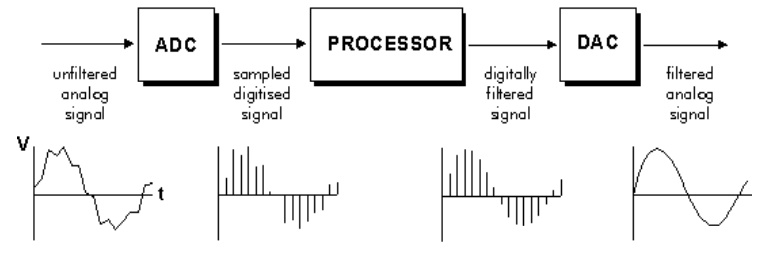
BASIC BLOCK DIAGRAM OF DIGITAL FILTERS

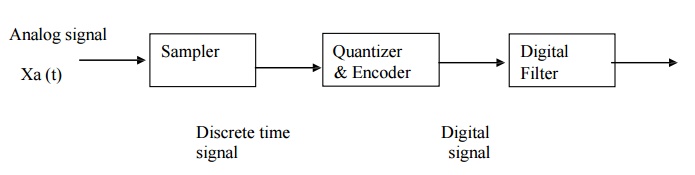
a.   Samplers are used for converting continuous time signal into a discrete time signal by taking samples of the continuous time signal at discrete time instants.

b.   The Quantizer are used for converting a discrete time continuous amplitude signal into a digital signal by expressing each sample value as a finite number of digits.

c.   In the encoding operation, the quantization sample value is converted to the binary equivalent of that quantization level.

d.   The digital filters are the discrete time systems used for filtering of sequences.

e.   These digital filters performs the frequency related operations such as low pass, high pass, band pass and band reject etc. These digital Filters are designed with digital hardware and software and are represented by difference equation.

DIFFERENCE BETWEEN ANALOG FILTER AND DIGITAL FILTER

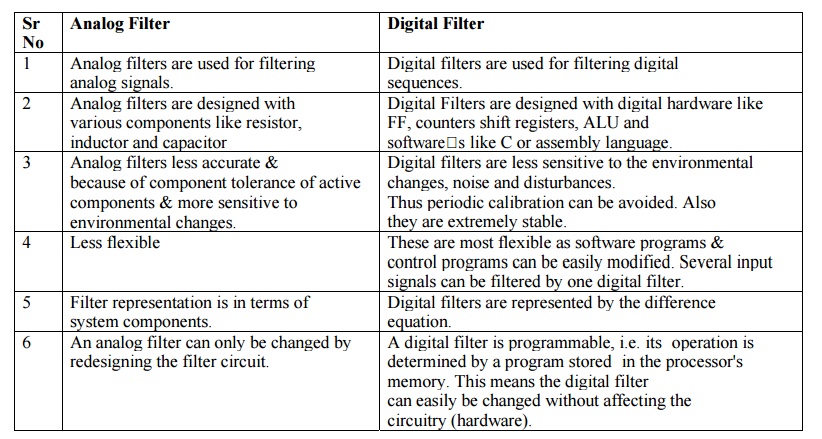
Analog Filter

1    Analog filters are used for filtering analog signals.

2    Analog filters are designed with various components like resistor, inductor and capacitor

3    Analog filters less accurate & because of component tolerance of active components & more sensitive to environmental changes.

4    Less flexible

5    Filter representation is in terms of system components.

6    An analog filter can only be changed by redesigning the filter circuit.

Digital Filter

1    Digital filters are used for filtering digital sequences.

2    Digital Filters are designed with digital hardware like FF, counters shift registers, ALU and software s like C or assembly language.

3    Digital filters are less sensitive to the environmental changes, noise and disturbances. Thus periodic calibration can be avoided. Also they are extremely stable.

4    These are most flexible as software programs & control programs can be easily modified. Several input signals can be filtered by one digital filter.

5    Digital filters are represented by the difference equation.

6    A digital filter is programmable, i.e. its operation is determined by a program stored in the processor's memory. This means the digital filter can easily be changed without affecting the circuitry (hardware).

FILTER TYPES AND IDEAL FILTER CHARACTERISTIC

 Filters are usually classified according to their frequency-domain characteristic as lowpass, highpass, bandpass and bandstop filters.

Lowpass Filter

A lowpass filter is made up of a passband and a stopband, where the lower frequencies Of the input signal are passed through while the higher frequencies are attenuated.

Highpass Filter

A highpass filter is made up of a stopband and a passband where the lower frequencies of the input signal are attenuated while the higher frequencies are passed.

Bandpass Filter

A bandpass filter is made up of two stopbands and one passband so that the lower and higher frequencies of the input signal are attenuated while the intervening frequencies are passed.

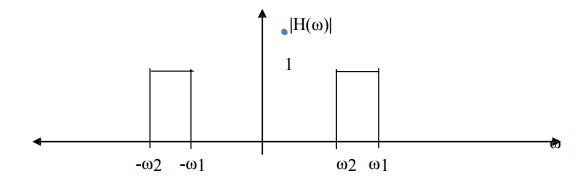
Bandstop Filter

A bandstop filter is made up of two passbands and one stopband so that the lower and higher frequencies of the input signal are passed while the intervening frequencies are attenuated. An idealized bandstop filter frequency response has the following

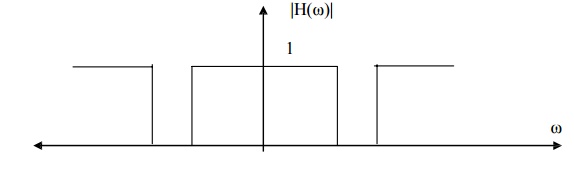
Multipass Filter

A multipass filter begins with a stopband followed by more than one passband. By default, a multipass filter in Digital Filter Designer consists of three passbands and

four stopbands. The frequencies of the input signal at the stopbands are attenuated while those at the passbands are passed.

Multistop Filter

A multistop filter begins with a passband followed by more than one stopband. By default, a multistop filter in Digital Filter Designer consists of three passbands and two stopbands.

All Pass Filter

An all pass filter is defined as a system that has a constant magnitude response for all frequencies.

|H(ω)| = 1                                   for 0 ≤ ω < ∏

The simplest example of an all pass filter is a pure delay system with system function H(z) = Z^-k. This is a low pass filter that has a linear phase characteristic.

All Pass filters find application as phase equalizers. When placed in cascade with a system that has an undesired phase response, a phase equalizers is designed to

compensate for the poor phase characteristic of the system and therefore to produce an overall linear phase response.

IDEAL FILTER CHARACTERISTIC

1.   Ideal filters have a constant gain (usually taken as unity gain) passband characteristic and zero gain in their stop band.

2.   Ideal filters have a linear phase characteristic within their passband.

3.   Ideal filters also have constant magnitude characteristic.

4.   Ideal filters are physically unrealizable.