Important Short Questions and Answers: Frequency Transformations

FREQUENCY TRANSFORMATIONS

1. Define DTFT.

2. Define Periodicity of DTFT.

3. Difference between DTFT and other transform.

The DFT and the DTFT can be viewed as the logical result of applying the standard continuous Fourier transform to discrete data. From that perspective, we have the satisfying result that it's not the transform that varies; it's just the form of the input:

·           If it is discrete, the Fourier transform becomes a DTFT.

·           If it is periodic, the Fourier transform becomes a Fourier series.

·           If it is both, the Fourier transform becomes a DFT.

4. Write about symmetry property of DTFT.

The Fourier Transform can be decomposed into a real and imaginary or into even and odd.

5. Define DFT pair.

The sequence of N complex numbers x₀, ..., x_N−1 is transformed into the sequence of N complex numbers X₀, ..., X_N−1 by the DFT according to the formula:

6.How will you express IDFT interms of DFT.

A useful property of the DFT is that the inverse DFT can be easily expressed in terms of the (forward) DFT, via several well-known "tricks". (For example, in computations, it is often convenient to only implement a fast Fourier transform corresponding to one transform direction and then to get the other transform direction from the first.) First, we can compute the inverse DFT by reversing the inputs:

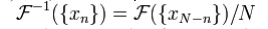
(As usual, the subscripts are interpreted modulo N; thus, for n = 0, we have x_{N − 0} = x₀.) Second, one can also conjugate the inputs and outputs:

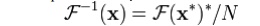
Third, a variant of this conjugation trick, which is sometimes preferable because it requires no modification of the data values, involves swapping real and imaginary parts (which can be done on a computer simply by modifying pointers). Define swap(x_n) as x_n with its real and imaginary parts swapped—that is, if x_n = a + bi then swap(x_n) is b + ai. Equivalently, swap(x_n) equals ix*_n .

Then

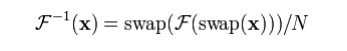
7.Write about Bilateral Z transform.

The bilateral or two-sided Z-transform of a discrete-time signal x[n] is the function X(z) defined as

where n is an integer and z is, in general, a complex number: 

z = Ae^jφ (OR)

z = A(cosjφ + sinjφ)

where A is the magnitude of z, and φ is the complex argument (also referred to as angle or phase) in radians

8. Write about Unilateral Z transforms.

Alternatively, in cases where x[n] is defined only for n ≥ 0, the single-sided or unilateral Z-transform is defined as

In signal processing, this definition is used when the signal is causal.

 9. Define Region Of Convergence.

The region of convergence (ROC) is the set of points in the complex plane for which the Z-transform

summation converges.

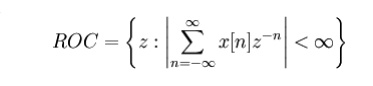
10.Write about the output response of Z transform

 11. Define Twiddle Factor.

A twiddle factor, in fast Fourier transform (FFT) algorithms, is any of the trigonometric constant coefficients that are multiplied by the data in the course of the algorithm.

12. State the condition for existence of DTFT?

The conditions are, If x(n)is absolutely summable then |x(n)|< If x(n) is not absolutely summable then it should have finite energy for DTFT to exit.

13. List the properties of DTFT.

Periodicity, Linearity, Time shift, Frequency shift, Scaling, Differentiation in frequency domain, Time reversal, Convolution, Multiplication in time domain, Parseval’s theorem

14. What is the DTFT of unit sample?

The DTFT of unit sample is 1 for all values of w.

15. Define Zero padding.

The method of appending zero in the given sequence is called as Zero padding.

16. Define circularly even sequence.

A Sequence is said to be circularly even if it is symmetric about the point zero on the circle. x(N-n)=x(n),1<=n<=N-1.

17. Define circularly odd sequence.

A Sequence is said to be circularly odd if it is anti symmetric about point x(0) on the circle

 18. Define circularly folded sequences.

A circularly folded sequence is represented as x((-n))N. It is obtained by plotting x(n) in clockwise direction along the circle.

19. State circular convolution.

This property states that multiplication of two DFT is equal to circular convolution of their sequence in time domain.

20. State parseval’s theorem.

Consider the complex valued sequences x(n) and y(n).If

x(n) - > X(k), y(n)ÆY(k) then x(n)y*(n)=1/N X(k)Y*(k)

21. Define Z transform.

The Z transform of a discrete time signal x(n) is denoted by X(z) and is given by X(z)= x(n)Z-n.

22. Define ROC.

The value of Z for which the Z transform converged is called region of convergence.

23. Find Z transform of x(n)={1,2,3,4}

x(n)= {1,2,3,4}

X(z)= x(n)z-n

=1+2z-1+3z-2+4z-3.

=1+2/z+3/z2+4/z3.

24. State the convolution property of Z transforms.

The convolution property states that the convolution of two sequences in time domain is equivalent to multiplication of their Z transforms.

25. What z transform of (n-m)?

By time shifting property

Z[A (n-m)]=AZ-m sinZ[ (n)] =1

26.State initial value theorem.

If x(n) is causal sequence then its initial value is given by x(0)=lim X(z)

27.List the methods of obtaining inverse Z transform.

Partial fraction expansion.

Contour integration

Power series expansion

Convolution.

28. Obtain the inverse z transform of X(z)=1/z-a,|z|>|a|

Given X(z)=z-1/1-az-1

By time shifting property X(n)=an.u(n-1)

1, Determine the 8-Point DFT of the Sequence x(n)={1,1,1,1,1,1,0,0}

 Soln:

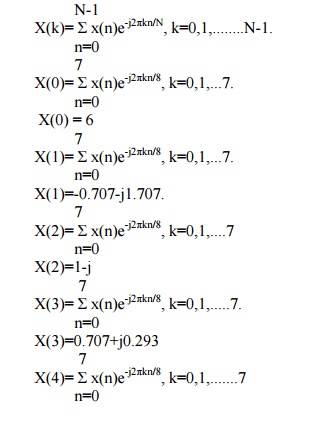
2, Determine the 8-Point DFT of the Sequence x(n)={1,1,1,1,1,1,1,1}

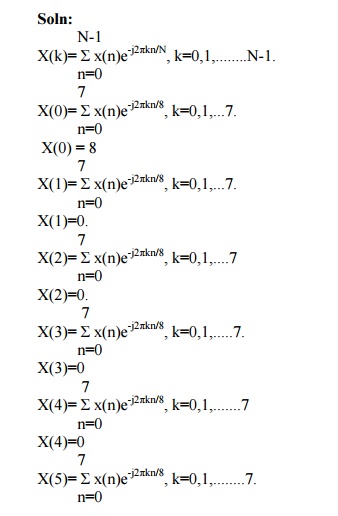
3, Determine the 8-Point DFT of the Sequence x(n)={1,2,3,4,4,3,2,1}

4, Determine the 8-Point IDFT of the Sequence x(n)={5,0,1-j,0,1,0,1+j,0}

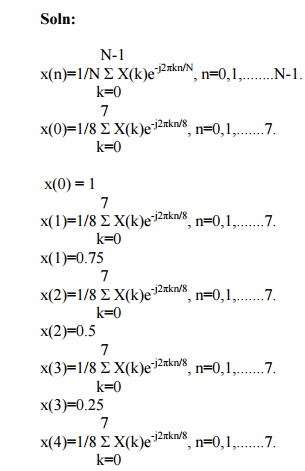
GLOSSARY:

The Transform that used to analyze the signals or systems Characteristics in frequency domain , which is difficult in case of Time Domain.

Laplace Transform:

Laplace Transform is the basic continuous Transform. Then it is developed to represent the continuous signals in frequency domain.

Discrete Time Fourier Transform:

For analyzing the discrete signals, the DTFT (Discrete Time Fourier Transform) is used. The output, that the frequency is continuous in DTFT. But the Transformed Value should be discrete. Since the Digital Signal Processors cannot work with the continuous frequency signals. So the DFT is developed to represent the discrete signals in discrete frequency domain.

Discrete Fourier Transform:

Discrete Fourier Transform is used for transforming a discrete time sequence of finite length “N” into a discrete frequency sequence of the same finite length “N”.

Periodicity:

If a discrete time signal is periodic then its DFT is also periodic. i.e. if a signal or sequence is repeated after N Number of samples, then it is called periodic signal.

Symmetry:

If a signal or sequence is repeated its waveform in a negative direction after “N/2” number of Samples, then it is called symmetric sequence or signal.

Linearity:

A System which satisfies the superposition principle is said to be a linear system. The DFT have the Linearity property. Since the DFT of the output is equal to the sum of the DFT’s of the Inputs.

Fast Fourier Transform:

Fast Fourier Transform is an algorithm that efficiently computes the discrete fourier transform of a sequence x(n). The direct computation of the DFT requires 2N² evaluations of trignometric functions. 4N² real multiplications and 4N(N-1) real additions.