Chapter: Digital Signal Processing : Frequency Transformations
Decimation In Frequency (DIFFFT)
DECIMATION IN FREQUENCY (DIFFFT)
In DIF N Point DFT is splitted into N/2 points
DFT s. X(k) is splitted with k even and k odd this is called Decimation in
frequency(DIF FFT).
N point DFT is given as
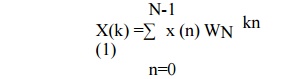
Since the sequence x(n) is splitted N/2 point
samples, thus

Let us split X(k) into even and odd numbered
samples
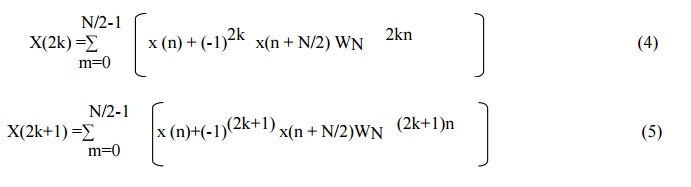
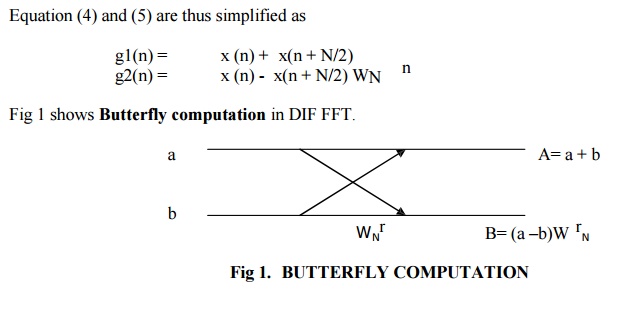
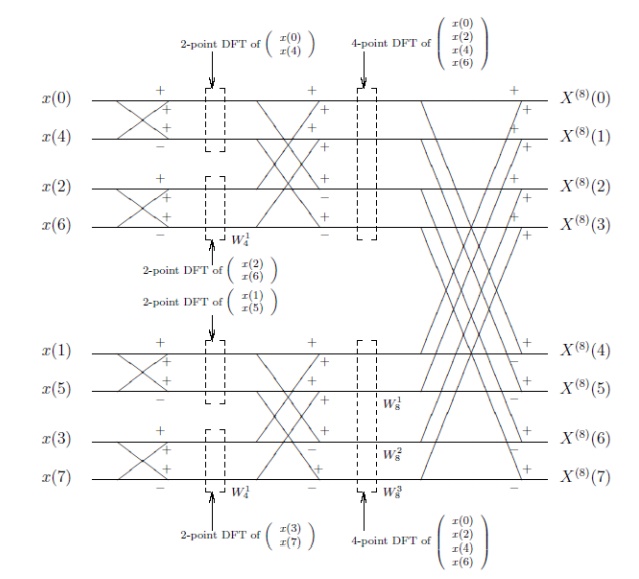
Fig 2 shows signal flow graph and
stages for computation of radix-2 DIF FFT algorithm of N=4

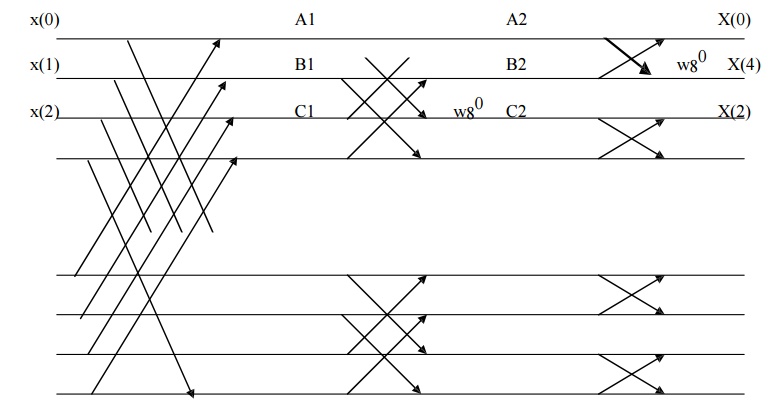
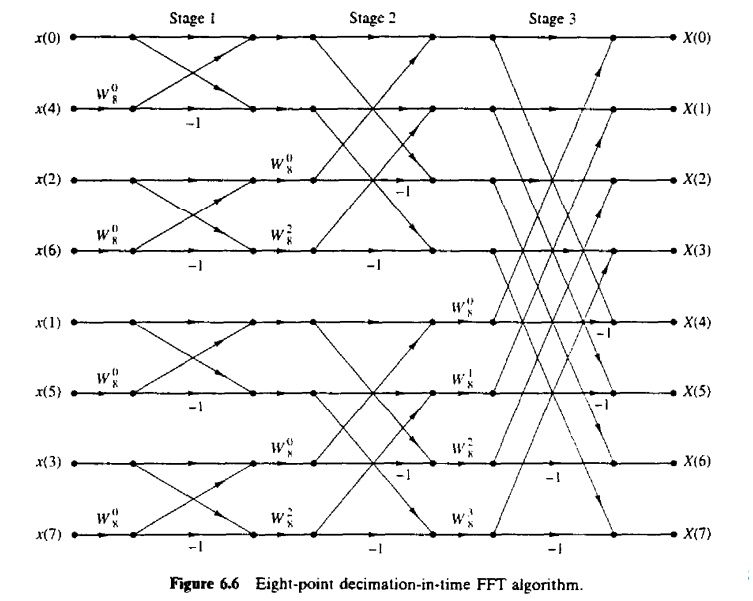
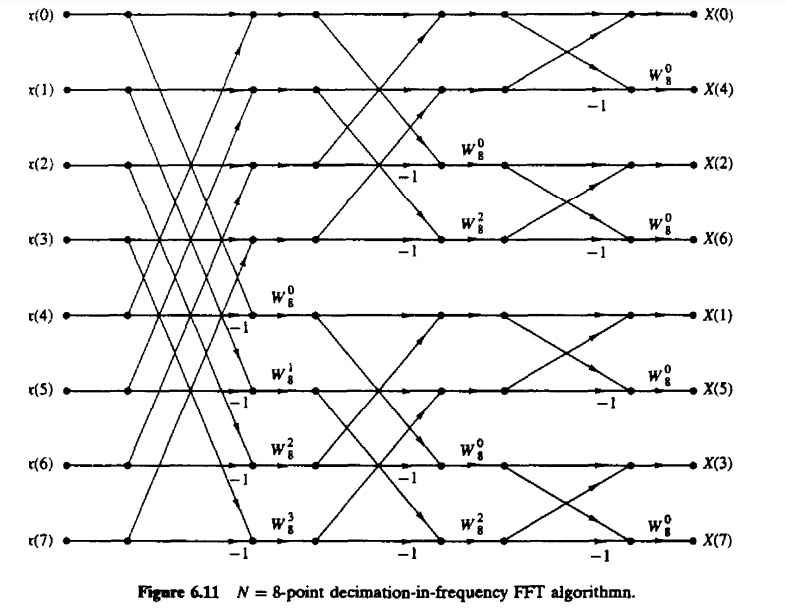
Fig 3 shows signal flow graph and
stages for computation of radix-2 DIF FFT algorithm of N=8

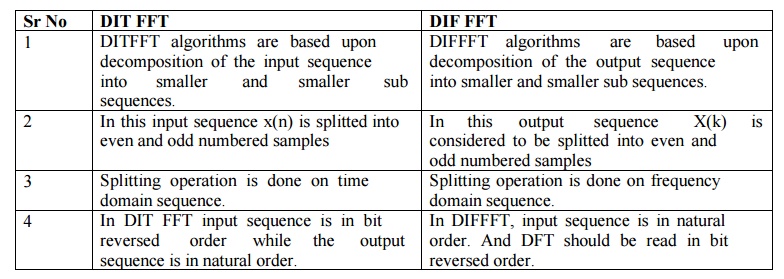
DIFFERENCE
BETWEEN DITFFT AND DIFFFT
DIT FFT
1. DITFFT
algorithms are based upon decomposition of the input sequence into smaller and
smaller sub sequences.
2. In
this input sequence x(n) is splitted into even and odd numbered samples
3.
Splitting operation is done on time domain sequence.
4. In DIT
FFT input sequence is in bit reversed order while the output sequence is in
natural order.
DIF FFT
1. DIFFFT
algorithms are based upon decomposition of the output sequence into smaller and
smaller sub sequences.
2. In
this output sequence X(k) is considered to be splitted into even and odd
numbered samples
3.
Splitting operation is done on frequency domain sequence.
4. In
DIFFFT, input sequence is in natural order. And DFT should be read in bit
reversed order.
DIFFERENCE BETWEEN DIRECT COMPUTATION & FFT

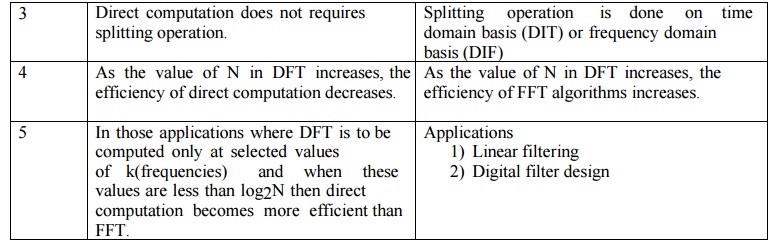
Direct Computation
1. Direct
computation requires large number of computations as compared with FFT
algorithms.
2.
Processing time is more and more for large number of N hence processor remains
busy.
3. Direct
computation does not requires splitting operation.
4. As the
value of N in DFT increases, the efficiency of direct computation decreases.
5. In
those applications where DFT is to be computed only at selected values of
k(frequencies) and when these values are less than log2N then direct
computation becomes more efficient than FFT.
Radix -2 FFT Algorithms
1.
Radix-2 FFT algorithms requires less number of computations.
2.
Processing time is less hence these algorithms compute DFT very quickly as
compared with direct computation.
3.
Splitting operation is done on time domain basis (DIT) or frequency domain
basis (DIF)
4. As the
value of N in DFT increases, the efficiency of FFT algorithms increases.
5.
Applications 1) Linear filtering 2) Digital filter design
Q)
x(n)={1,2,2,1} Find X(k) using DITFFT.
Q)
x(n)={1,2,2,1} Find X(k)using DIFFFT.
Q)
x(n)={0.3535,0.3535,0.6464,1.0607,0.3535,-1.0607,-1.3535,-0.3535} Find X(k)
using DITFFT.
Q) Using
radix 2 FFT algorithm, plot flow graph for N=8.
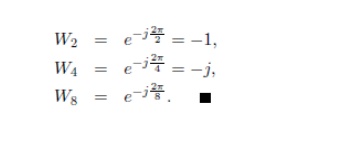

Related Topics