Frequency Response Characteristic

FREQUENCY RESPONSE CHARACTERISTIC

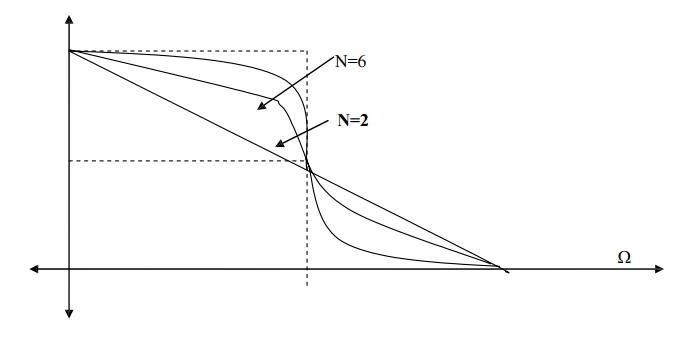
The frequency response characteristic of |Ha(Ω)|² is as shown. As the order of the filter N increases, the butterworth filter characteristic is more close to the ideal characteristic. Thus at higher orders like N=16 the butterworth filter characteristic closely approximate ideal filter characteristic. Thus an infinite order filter (N ∞) is required to get ideal characteristic.

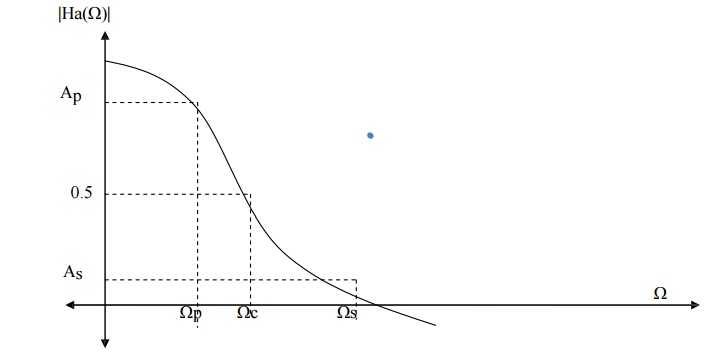
Ap= attenuation in passband.

As= attenuation in stopband.

Ωp = passband edge frequency

Ωs = stopband edge frequency

Specification for the filter is

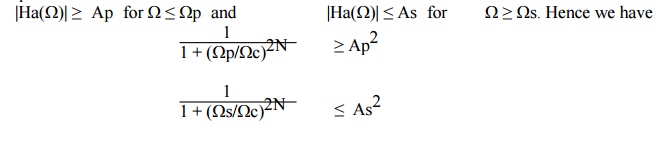
To determine the poles and order of analog filter consider equalities. 

Q) Design a digital filter using a butterworth approximation by using impulse invariance. 

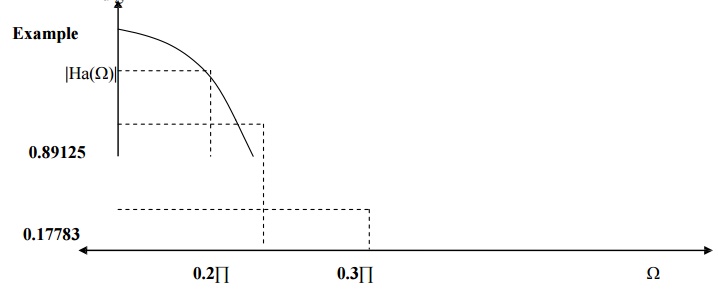
  Filter Type - Low Pass Filter           

Ap - 0.89125                

As  - 0.17783                

Ωp -  0.2∏          

Ωs -  0.3∏          

Step 1) To convert specification to equivalent analog filter.

(In impulse invariance method frequency relationship is given as ω= Ω T while in Bilinear transformation method frequency relationship is given as Ω= (2/T) tan (ω/2) If Ts is not specified consider as 1)

|Ha(Ω)| ≥ 0.89125 for Ω ≤ 0.2∏/T and       |Ha(Ω)| ≤ 0.17783 for    Ω ≥ 0.3∏/T.

Step 2) To determine the order of the filter.

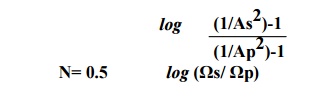
N= 5.88

1.   Order of the filter should be integer.

2.   Always go to nearest highest integer vale of N.

Hence N=6

Step 3) To find out the cutoff frequency (-3DB frequency)

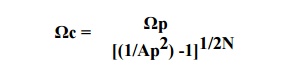
cutoff frequency Ωc = 0.7032

Step 4) To find out the poles of analog filter system function.

For stable filter all poles lying on the left side of s plane is selected. Hence

S1  = -0.182 + j 0.679               S1* = -0.182 - j 0.679

S2  = -0.497 + j 0.497                       S2* = -0.497 - j 0.497

S3  = -0.679 + j 0.182                         S3* = -0.679 - j 0.182

Step 5) To determine the system function (Analog Filter)

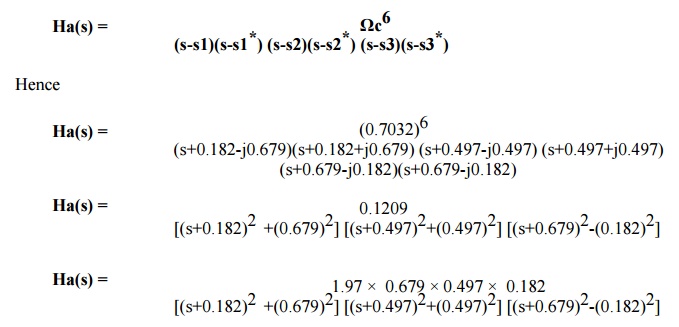
Step 6) To determine the system function (Digital Filter)

(In Bilinear transformation replace s by the term ((z-1)/(z+1)) and find out the transfer function of digital function)

Step 7) Represent system function in cascade form or parallel form if asked.

Q) Given for low pass butterworth filter

Ap= -1 db at 0.2∏

As= -15 db at 0.3∏

a)     Calculate N and Pole location

b)    Design digital filter using BZT method.

Q) Obtain transfer function of a lowpass digital filter meeting specifications

Cutoff 0-60Hz

Stopband > 85Hz

Stopband attenuation > 15 db

Sampling frequency= 256 Hz . use butterworth characteristic.

Q) Design second order low pass butterworth filter whose cutoff frequency is 1 kHz at sampling frequency of 10⁴ sps. Use BZT and Butterworth approximation.