Gas Mixtures

GAS MIXTURES

Pure substance is defined as a substance which means that it is homogeneous and unchanging in chemical composition.

COMPOSITION OF A GAS MIXTURE: MASS AND MOLE FRACTIONS

To determine the properties of a mixture, we need to know the composition of the mixture as well as the properties of the individual components. There are two ways to describe the composition of a mixture: either by specifying the number of moles of each component, called molar analysis, or by specifying the mass of each component, called gravimetric analysis.

Consider a gas mixture composed of k components. The mass of the mixture mm is the sum of the masses of the individual components, and the mole number of the mixture Nm is the sum of the mole numbers of the individual components.

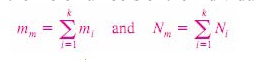
The ratio of the mass of a component to the mass of the mixture is called the mass fraction mf, and the ratio of the mole number of a component to the mole number of the mixture is called the mole fraction

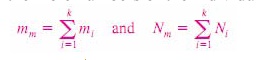
Dividing (1) by mm or (2) by Nm, we can easily show that the sum of the mass fractions or mole fractions for a mixture is equal to 1

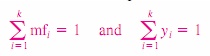
The mass of a substance can be expressed in terms of the mole number N and molar mass M of the substance as m _ NM. Then the apparent (oraverage) molar mass and the gas constant of a mixture can be expressed as

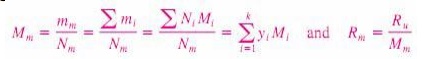
The molar mass of a mixture can also be expressed as

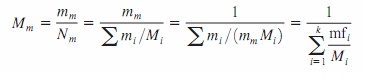
Mass and mole fractions of a mixture are related by

P-v-T BEHAVIOR OF GAS MIXTURES: IDEAL AND REAL GASES

An ideal gas is defined as a gas whose molecules are spaced far apart so that the behavior of a molecule is not influenced by the presence of other molecules—a situation encountered at low densities. We also mentioned that real gases approximate this behavior closely when they are at a low pressure or high temperature relative to their critical-point values. The P-v-T behavior of an ideal gas is expressed by the simple relation Pv _ RT, which is called the ideal-gas equation of state. The P-v-T behavior of real gases is expressed by more complex equations of state or by Pv _ ZRT, where Z is the compressibility factor.

When two or more ideal gases are mixed, the behavior of a molecule normally is not influenced by the presence of other similar or dissimilar molecules, and therefore a nonreacting mixture of ideal gases also behaves as an ideal gas. Air, for example, is conveniently treated as an ideal gas in the range where nitrogen and oxygen behave as ideal gases. When a gas mixture consists of real (nonideal) gases, however, the prediction of the P-v-T behavior of the mixture becomes rather involved.

The prediction of the P-v-T behavior of gas mixtures is usually based on two

models: Dalton’s   law   of   additive   pressures

Both models are described and discussed below.

Dalton’s  law   of   additive   pressures:

Dalton's law (also called Dalton's law of partial pressures) states that the total pressure exerted by a gaseous mixture is equal to the sum of the partial pressures of each individual component in a gas mixture. This empirical law was observed by John Dalton in 1801 and is related to the ideal gas laws. Mathematically, the pressure of a mixture of gases can be defined as the summation

Amagat’s law   of   additive   volumes:

Amagat's law or the Law of Partial Volumes of 1880 describes the behavior and properties of mixtures of ideal (as well as some cases of non-ideal) gases. Of use in chemistry and thermodynamics, Amagat's law states that the volume Vm of a gas mixture is equal to the sum of volumes Vi of the K component gases, if the temperature T and the pressure p remain the same:

This is the experimental expression of volume as an extensive quantity. It is named after Emile Amagat. Both Amagat's and Dalton's Law predict the properties of gas mixtures. Their predictions are the same for ideal gases. However, for real (non-ideal) gases, the results differ. Dalton's Law of Partial Pressures assumes that the gases in the mixture are non-interacting (with each other) and each gas independently applies its own pressure, the sum of which is the total pressure. Amagat's Law assumes that the volumes of each component gas (same temperature and pressure) are additive; the interactions of the different gases are the same as the average interactions of the components.

Heat capacity

The heat capacity at constant volume of an ideal gas is:

It is seen that the constant is just the dimensionless heat capacity at constant volume. It is equal to half the number of degrees of freedom per particle. For

moderate temperatures, the constant for a monoatomic gas is Cv = 3/2 while for

a diatomic gas it Is Cv = 5/2  . It is seen that macroscopic measurements on heat capacity provide information on the microscopic structure of the molecules.

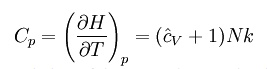
where H = U + pV is the enthalpy of the gas. It is seen that is also a constant and that the dimensionless heat capacities are related by:

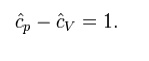
ENTROPY

Using the results of thermodynamics only, we can go a long way in determining the expression for the entropy of an ideal gas. This is an important step since, according to the theory of thermodynamic potentials, of which the internal energy U is one, if we can express the entropy as a function of U and the volume V, then we will have a complete statement of the thermodynamic behavior of the ideal gas. We will be able to derive both the ideal gas law and the expression for internal energy from it. Since the entropy is an exact differential, using the chain rule, the change in entropy when going from a reference state 0 to some other state with entropy S may be written asS where:

This is about as far as we can go using thermodynamics alone. Note that the above equation is flawed — as the temperature approaches zero, the entropy approaches negative infinity, in contradiction to the third law of thermodynamics. In the above "ideal" development, there is a critical point, not at absolute zero, at which the argument of the logarithm becomes unity, and the entropy becomes zero.