Chapter: Mechanical : Dynamics of Machines : Force Analysis
Forces on the Reciprocating Parts of an Engine, Neglecting the Weight of the Connecting Rod
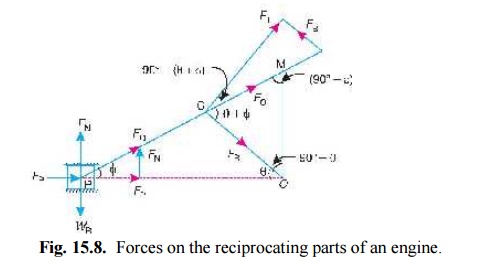
FORCES ON THE RECIPROCATING PARTS OF AN ENGINE, NEGLECTING THE WEIGHT OF THE CONNECTING ROD
The various forces acting on the reciprocating parts of a horizontal engine are shown in Fig. 15.8. The expressions for these forces, neglecting the weight of the connecting rod, may be derived as discussed below :
1. Piston effort. It is the net force acting on the piston or crosshead pin, along the line of stroke. It is denoted by Fp in Fig. 15.8.
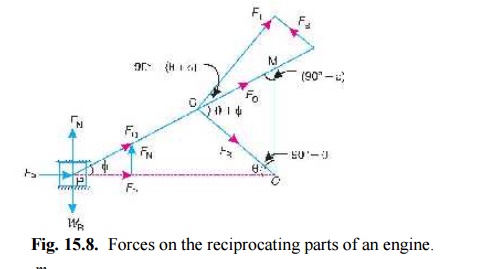
Fig. 15.8. Forces on the reciprocating parts of an engine.

WR = Weight of the reciprocating parts in newtons = mR.g
We know that acceleration of the reciprocating parts,

Accelerating force or inertia force of the reciprocating parts,
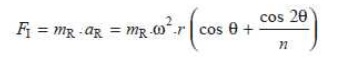
It may be noted that in a horizontal engine, the reciprocating parts are accelerated from rest, during the latter half of the stroke (i.e. when the piston moves from inner dead centre to outer dead centre). It is, then, retarded during the latter half of the stroke (i.e. when the piston moves from outer dead centre to inner dead centre). The inertia force due to the acceleration of the reciprocating parts, opposes the force on the piston due to the difference of pressures in the cylinder on the two sides of the piston. On the other hand, the inertia force due to retardation of the reciprocating parts, helps the force on the piston.

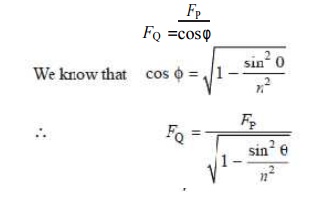
2. Force acting along the connecting rod. It is denoted by FQ in Fig. 15.8. From the geom-etry of the figure, we find that
3. Thrust on the sides of the cylinder walls or normal reaction on the guide bars. It is denoted by FN in Fig. 15.8. From the figure, we find that
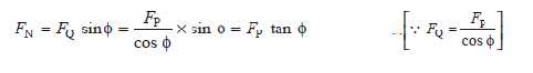
4. Crank-pin effort and thrust on crank shaft bearings. The force acting on the connecting rod FQ may be resolved into two components, one perpendicular to the crank and the other along the crank. The component of FQ perpendicular to the crank is known as crank-pin effort and it is denoted by FT in Fig. 15.8. The component of FQ along the crank produces a thrust on the crank shaft bearings and it is denoted by FB in Fig. 15.8.
Resolving FQ perpendicular to the crank,
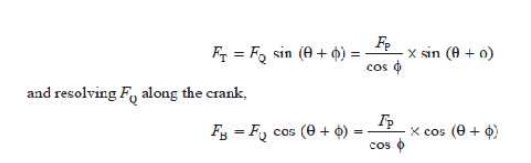
5. Crank effort or turning moment or torque on the crank shaft. The product of the crank-pin effort (FT) and the crank pin radius (r) is known as crank effort or turning moment or torque on the crank shaft.
Mathematically,

Q. The crank-pin circle radius of a horizontal engine is 300 mm. The mass of the reciprocating parts is 250 kg. When the crank has travelled 60┬░ from I.D.C., the difference between the driving and the back pressures is 0.35 N/mm2. The connecting rod length between centres is 1.2 m and the cylinder bore is 0.5 m. If the engine runs at 250 r.p.m. and if the effect of piston rod diameter is neglected, calculate : 1. pressure on slide bars, 2. thrust in the connecting rod, 3. tangential force on the crank-pin, and 4. turning moment on the crank shaft.
Solution. Given: r = 300 mm = 0.3 m ; mR = 250 kg; ╬Ė = 60┬░; p1 ŌĆō p2 = 0.35 N/mm2; l =
1.2 m ; D = 0.5 m = 500 mm ; N = 250 r.p.m. or Žē = 2 ŽĆ ├Ś 250/60 = 26.2 rad/s First of all, let us find out the piston effort (FP).
We know that net load on the piston,

1. Pressure on slide bars
Let Žå = Angle of inclination of the connecting rod to the line of stroke.
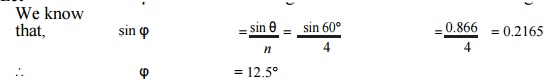
We know that pressure on the slide bars,
FN = FP tan Žå = 49.424 ├Ś tan 12.5┬░ = 10.96 kN Ans.
2. Thrust in the connecting rod
We know that thrust in the connecting rod,
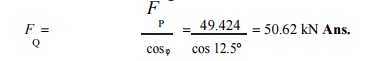
3. Tangential force on the crank-pin
We know that tangential force on the crank pin,
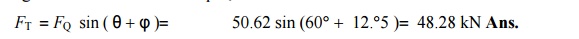
4. Turning moment on the crank shaft
We know that turning moment on the crank shaft,

Q. The crank and connecting rod of a petrol engine, running at 1800 r.p.m.are 50 mm and 200 mm respectively. The diameter of the piston is 80 mm and the mass of the reciprocating parts is 1 kg. At a point during the power stroke, the pressure on the piston is 0.7 N/mm2, when it has moved 10 mm from the inner dead centre. Determine : 1. Net load on the gudgeon pin, 2. Thrust in the connecting rod, 3. Reaction between the piston and cylinder, and 4. The engine speed at which the above values become zero.
Solution. Given : N = 1800 r.p.m. or Žē = 2ŽĆ ├Ś 1800/60 = 188.52 rad/s ; r = 50 mm = 0.05 m; l = 200 mm ; D = 80 mm ; mR = 1 kg ; p = 0.7 N/mm2 ; x = 10 mm
1. Net load on the gudgeon pin
We know that load on the piston,
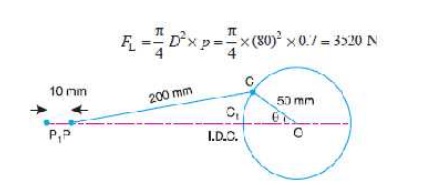
When the piston has moved 10 mm from the inner dead centre, i.e. when P1P = 10 mm, the crank rotates from OC1 to OC through an angle ╬Ė as shown in Fig. 15.10.
By measurement, we find that *╬Ė = 33┬░.
We know that ratio of lengths of connecting rod and crank,
n = l/r = 200 /50 = 4
and inertia force on the reciprocating parts,
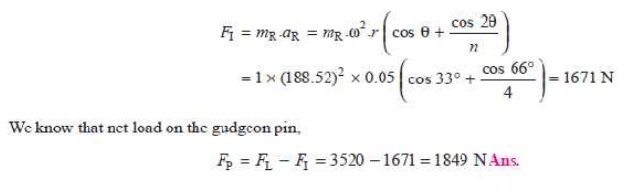
2. Thrust in the connecting rod

We know that thrust in the connecting rod,
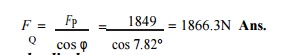
3. Reaction between the piston and cylinder
We know that reaction between the piston and cylinder,
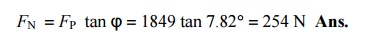
4. Engine speed at which the above values will become zero
A little consideration will show that the above values will become zero, if the inertia force on the reciprocating parts (F1) is equal to the load on the piston (FL). Let Žē 1 be the speed in rad/s, at which FI = FL .
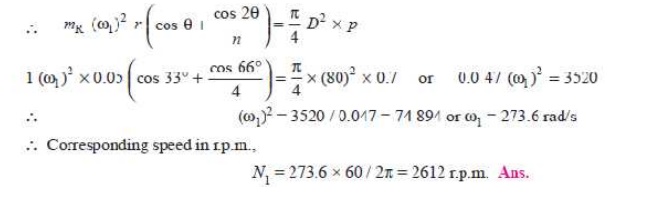
Q. A vertical petrol engine 100 mm diameter and 120 mm stroke has a connecting rod 250 mm long. The mass of the piston is 1.1 kg. The speed is 2000 r.p.m. On the expansion stroke with a crank 20┬░ from top dead centre, the gas pressure is 700 kN/m2. Determine:
1.Net force on the piston, 2. Resultant load on the gudgeon pin, 3.Thrust
on the cylinder walls, and 4. Speed above which, other things re-maining same,
the gudgeon pin load would be reversed in direction.
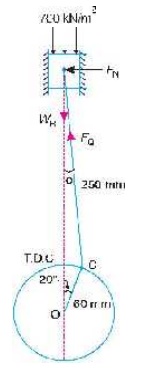
Solution. Given: D = 100 mm = 0.1 m ; L = 120 mm = 0.12 m or r = L/2 =
0.06 m ; l = 250 mm = 0.25 m ; mR = 1.1 kg ; N = 2000 r.p.m. or
Žē = 2 ŽĆ ├Ś 2000/60 = 209.5 rad/s ; ╬Ė = 20┬░; p = 700 kN/m2
1. Net force on the piston
The configuration diagram of a vertical engine is shown in Fig. 15.11.
We know that force due to gas pressure,

We know that for a vertical engine, net force on the piston,
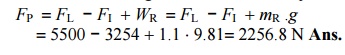
2. Resultant load on the gudgeon pin
Let Žå = Angle
of inclination of the connecting rod to the line of stroke. We know that,
sin Žå = sin ╬Ė / n = sin 20┬░/4.17 = 0.082 Ōł┤ Žå = 4.7┬░
We know
that resultant load on the gudgeon pin,
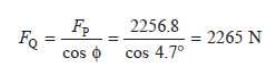
3. Thrust
on the cylinder walls
We know that thrust on the cylinder
walls,
FN = FN
tan Žå = 2256.8 . tan 4.o 7 = 185.5 N Ans.
4. Speed, above which, the gudgeon pin load
would be reversed in direction
Let N1 = Required speed, in r.p.m.
The
gudgeon pin load i.e. F Q will be reversed in direction, if FQ
becomes negative. This is only possible when FP is negative.
Therefore, for FP to be negative, FI must be greater than
(FL + W R),
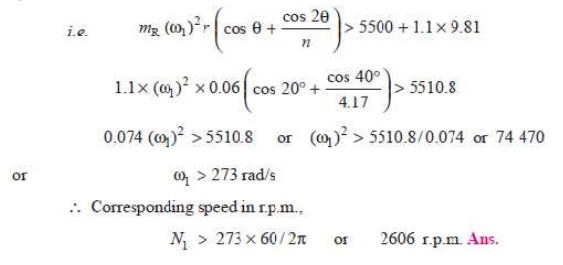
Q. A horizontal steam engine running at 120 r.p.m. has a bore of 250 mm and a stroke of 400 mm. The connecting rod is 0.6 m and mass of the reciprocating parts is 60 kg. When the crank has turned through an angle of 45┬░ from the inner dead centre, the steam pressure on the cover end side is 550 kN/m2 and that on the crank end side is 70 kN/m2. Considering the diameter of the piston rod equal to 50 mm, determine: 1. turning moment on the crank shaft, 2. thrust on the bearings, and 3. acceleration of the flywheel, if the power of the engine is 20 kW, mass of the flywheel 60 kg and radius of gyration 0.6 m.
Solution. Given : N = 120 r.p.m. or Žē = 2ŽĆ ├Ś 120/60 = 12.57 rad/s ; D = 250 mm = 0.25 m ;
L = 400 mm = 0.4 m or r =
L/2 = 0.2 m ; l = 0.6 m ; mR
= 60 kg ; ╬Ė = 45┬░ ; d = 50 mm = 0.05 m ; p1
= 550 kN/m2 = 550 ├Ś 10 3 N/m2 ; p2
= 70 kN/m2 = 70 ├Ś 10 3 N/m2
1. Turning moment on the
crankshaft
First of all, let us find the net load on the
piston (FP).
We know
that area of the piston on the cover end side,

2. Thrust on the bearings
We know
that thrust on the bearings,

3. Acceleration of the flywheel
Given: P
= 20 kW = 20 ├Ś 10 3 W; m =
60 kg ; k = 0.6 m
Let ╬▒ = Acceleration of the flywheel in rad/s2.
We know
that mass moment of inertia of the flywheel,
I = m.k2 = 60 ├Ś (0.6) 2 = 21.6 kg-m2
Ōł┤ Accelerating torque, TA = I.╬▒ = 21.6 ╬▒ N-m ...(i)
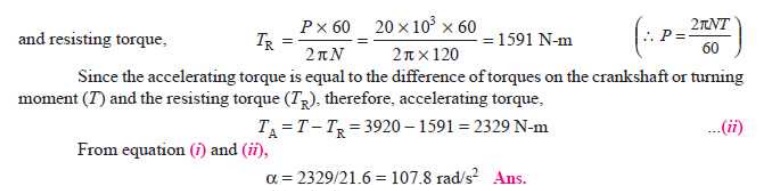
Related Topics