Fluctuation of Energy

FLUCTUATION OF ENERGY

The fluctuation of energy may be determined by the turning moment diagram for one complete cycle of operation. Consider the turning moment diagram for a single cylinder double acting steam engine as shown in Fig. 16.1. We see that the mean resisting torque line AF cuts the turning moment diagram at points B, C, D and E. When the crank moves from a to p, the work done by the engine is equal to the area aBp , whereas the energy required is represented by the area aABp. In other words, the engine has done less work (equal to the area a AB) than the requirement. This amount of energy is taken from the flywheel and hence the speed of the flywheel decreases. Now the crank moves from p to q, the work done by the engine is equal to the area pBbCq, whereas the requirement of energy is represented by the area pBCq. Therefore, the engine has done more work than the requirement. This excess work (equal to the area BbC) is stored in the flywheel and hence the speed of the flywheel increases while the crank moves from p to q.

Similarly, when the crank moves from q to r, more work is taken from the engine than is developed. This loss of work is represented by the area C c D. To supply this loss, the flywheel gives up some of its energy and thus the speed decreases while the crank moves from q to r. As the crank moves from r to s, excess energy is again developed given by the area D d E and the speed again increases. As the piston moves from s to e, again there is a loss of work and the speed decreases. The variations of energy above and below the mean resisting torque line are called fluctuations of energy. The areas BbC, CcD, DdE, etc. represent fluctuations of energy.

A little consideration will show that the engine has a maximum speed either at q or at s. This is due to the fact that the flywheel absorbs energy while the crank moves from p to q and from r to s. On the other hand, the engine has a minimum speed either at p or at r. The reason is that the flywheel gives out some of its energy when the crank moves from a to p and q to r. The difference between the maximum and the minimum energies is known as maximum fluctuation of energy.

1 Determination of Maximum Fluctuation of Energy

A turning moment diagram for a multi-cylinder engine is shown by a wavy curve in Fig. 16.4. The horizontal line A G represents the mean torque line. Let a1, a3, a5 be the areas above the mean torque line and a2, a4 and a6 be the areas below the mean torque line. These areas represent some quantity of energy which is either added or subtracted from the energy of the moving parts of the engine

Let the energy in the flywheel at A = E, then from Fig. 16.4, we have

Energy at B = E + a1 Energy at C = E + a1– a2

Energy at D = E + a1 – a2 + a3 Energy at E = E + a1 – a2 + a3 – a4

Energy at F = E + a 1 – a2 + a3 – a4 + a5 Energy at G = E + a1 – a2 + a3 – a4 + a5 – a6 = Energy at A (i.e. cycle repeats after G)

Let us now suppose that the greatest of these energies is at B and least at E. Therefore, Maximum energy in flywheel

= E + a1 Minimum energy in the flywheel

= E + a1 – a2 + a3 – a4

∴ Maximum fluctuation of energy,

∆ E = Maximum energy – Minimum energy

= (E + a₁) – (E + a₁ – a₂ + a₃ – a₄) = a₂ – a₃ + a₄

Fig. 16.4. Determination of maximum fluctuation of energy.

2 Coefficient of Fluctuation of Energy

It may be defined as the ratio of the maximum fluctuation of energy to the work done per cycle. Mathematically, coefficient of fluctuation of energy,

CE = Maximum fluctuation of energy / Work done per cycle

The work done per cycle (in N-m or joules) may be obtained by using the following two

Relations

1. Work done per cycle = Tmean × θ

The mean torque (Tmean) in N-m may be obtained by using the following relation :

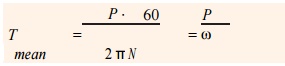
where          P = Power transmitted in watts,

          N = Speed in r.p.m., and

          ω = Angular speed in rad/s = 2 Ï€ N/60

2. The work done per cycle may also be obtained by using the following relation :

where          n = Number of working strokes per minute,

= N, in case of steam engines and two stroke internal combustion engines,

= N /2, in case of four stroke internal combustion engines.

The following table shows the values of coefficient of fluctuation of energy for steam engines and internal combustion engines.

Coefficient of fluctuation of energy (C_E) for steam and internal combustion engines.