Chapter: Mechanical : Dynamics of Machines : Force Analysis
Correction Couple to be Applied to Make two Mass System Dynamically Equivalent
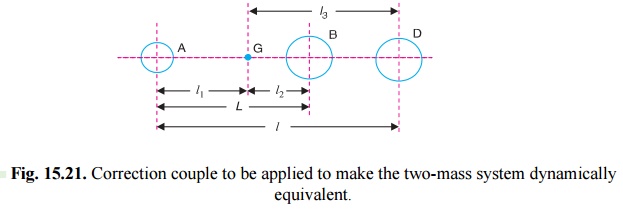
CORRECTION COUPLE TO BE APPLIED TO MAKE TWO MASS SYSTEM DYNAMICALLY EQUIVALENT
In
Art. 15.11, we have discussed the conditions for equivalent dynamical system of
two bodies. A little consideration will show that when two masses are placed
arbitrarily*, then the conditions (i)
and (ii) as given in Art. 15.11 will
only be satisfied. But the condition (iii)
is not possible to satisfy. This means that the mass moment of inertia of these
two masses placed arbitrarily, will differ than that of mass moment of inertia
of the rigid body.
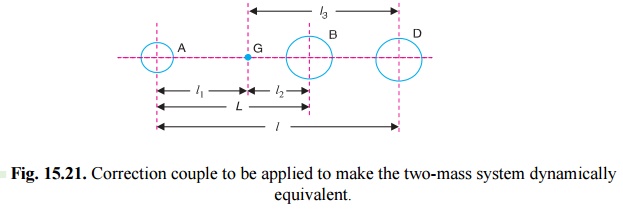
Fig. 15.21. Correction couple to be applied to make the two-mass system
dynamically equivalent.
Consider
two masses, one at A and the other at
D be placed arbitrarily, as shown in
Fig
15.21.
Let l3 = Distance of mass placed
at D from G,
l1= New mass moment of inertia of the two
masses;

The difference of the torques T' is known as correction couple. This
couple must be applied, when the masses are placed arbitrarily to make the
system dynamical equivalent. This, of course, will satisfy the condition (iii)
Q. A connecting rod of an I.C. engine
has a mass of 2 kg and the distance between the centre of gudgeon pin and centre
of crank pin is 250 mm. The C.G. falls at a point 100 m m from the gudgeon pin
along the line of centres. The radius of gyration about an axis through the
C.G. perpendicular to the plane of rotation is 110 mm. Find the equivalent
dynamical system if only one of the masses is located at gudgeon pin.
If the connecting rod is replaced by two masses, one at the
gudgeon pin and the other at the crank pin and the angular acceleration of the
rod is 23 000 rad/s2 clockwise, determine the correc- tion couple applied
to the system to reduce it to a dynamically equivalent system.
Solution. Given : m
= 2 kg ; l = 250 mm = 0.25 m ; l1 = 100 mm = 0.1m ; kG = 110 mm = 0.11 m ; α= 23 000 rad/s2
Equivalent dynamical system
It is given that one of the masses
is located at the gudgeon pin. Let the other mass be located at a distance l2 from the centre of
gravity. We know that for an equivalent dynamical system.
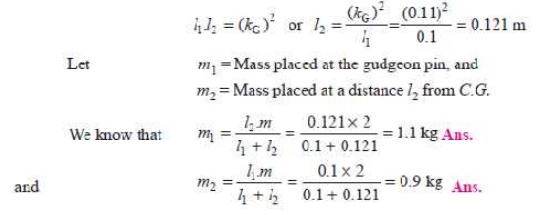
Correction couple
Since the connecting rod is replaced
by two masses located at the two centres (i.e.
one at the gudgeon pin and the other at the crank pin), therefore,
l
= 0.1 m, and l3 = l – l1 = 0.25 – 0.1 = 0.15 m
Let k1 = New radius of gyration.
We know that (k1)2=
l1.l3 = 0.1 Ă— 0.15 = 0.015 m 2
Correction couple,
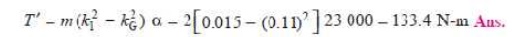
Related Topics