Chapter: Mechanical : Dynamics of Machines : Force Analysis
Equivalent Dynamical System
EQUIVALENT DYNAMICAL SYSTEM
In order to determine the motion of a rigid body, under the
action of external forces, it is usually convenient to replace the rigid body
by two masses placed at a fixed distance apart, in such a way that,
1.
the
sum of their masses is equal to the total mass of the body ;
2.
the
centre of gravity of the two masses coincides with that of the body ; and
3.
the
sum of mass moment of inertia of the masses about their centre of gravity is
equal to the mass moment of inertia of the body.
When
these three conditions are satisfied, then it is said to be an equivalent
dynamical system. Consider a rigid body, having its centre of gravity at G, as shown in Fig. 15.14.
Let m = Mass of the body,
kG = Radius of gyration about its centre of gravity G,
m1 and m 2 = Two masses which form a dynamical
equivalent system, l1 = Distance of mass m1 from G,
l2 = Distance of mass m2 from
G,
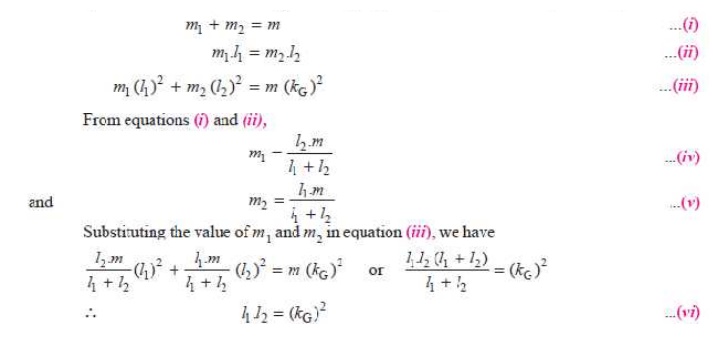
This
equation gives the essential condition of placing the two masses, so that the
system becomes dynamical equivalent. The distance of one of the masses (i.e. either l1 or l2)
is arbitrary chosen and the other distance is obtained from equation (vi).
Q.
A connecting rod is suspended from a point 25 mm above the
centre of small end, and 650 mm above its centre of
gravity, its mass being 37.5 kg. When permitted to oscil- late, the time period
is found to be 1.87 seconds. Find the dynamical equivalent system constituted
of two masses, one of which is located at the small end centre.
Solution. Given : h
= 650 mm = 0.65 m ; l1 = 650 ‚Äď 25 = 625 mm = 0.625 m ; m = 37.5 kg
; tp = 1.87 s
First of all, let us find the radius
of gyration (kG) of the
connect- ing rod (considering it is a compound pendulum), about an axis passing
through its centre of gravity, G.
We
know that for a compound pendulum, time period of oscillation (tp),

It is
given that one of the masses is located at the small end centre. Let the other
mass is located at a distance l2
from the centre of gravity G, as
shown in Fig. 15.19. We know that, for a dynamically equivalent system,
l1.l2 = (kG)2

Related Topics