Angular Velocity and Acceleration of the Connecting Rod

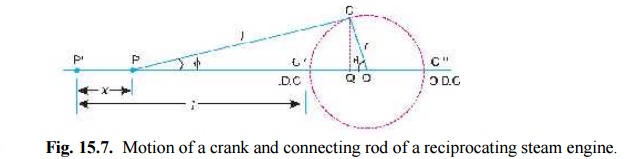
          Fig. 15.7. Motion of a crank and connecting rod of a reciprocating steam engine.

Let     l         =       Length of connecting rod between the centres,

          r        =       Radius of crank or crank pin circle,

          Ï† =    Inclination of connecting rod to the line of stroke PO, and

          n        =       Ratio of length of connecting rod to the radius of crank = l/r.

ANGULAR VELOCITY AND ACCELERATION OF THE CONNECTING ROD

Consider the motion of a connecting rod and a crank as shown in Fig. 15.7.From the geometry of the figure, we find that

CQ = l sin φ = r sin θ

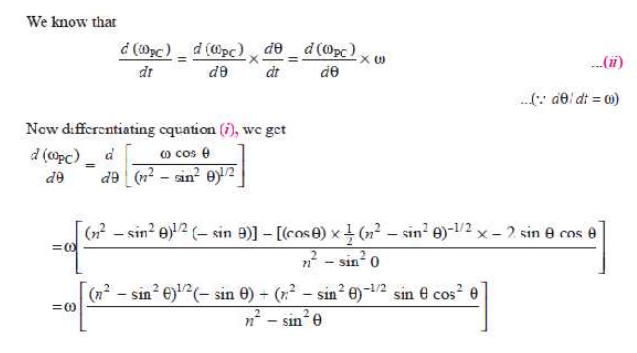
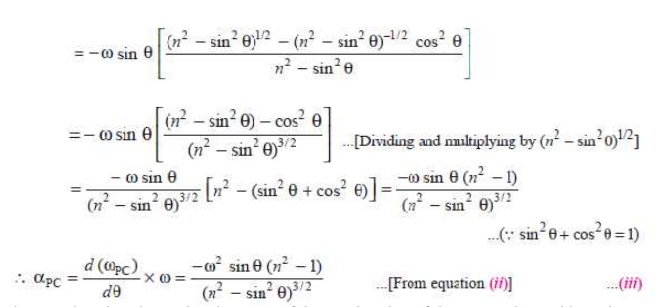
The negative sign shows that the sense of the acceleration of the connecting rod is such that it tends to reduce the angle φ..

Q.In a slider crank mechanism, the length of the crank and connecting rod are 150 mm and 600 mm respectively. The crank position is 60° from inner dead centre. The crank shaft speed is 450 r.p.m. (clockwise). Using analytical method, determine: 1. Velocity and acceleration of the slider, and 2. Angular velocity and angular acceleration of the connecting rod.

Solution. Given : r = 150 mm = 0.15 m ; l = 600 mm = 0.6 m ; Î¸ = 60°; N = 400 r.p.m or Ï‰ = Ï€ Ã— 450/60 = 47.13 rad/s

1. Velocity and acceleration of the slider

We know that ratio of the length of connecting rod and crank, 

n = l / r = 0.6 / 0.15 = 4