Finite Field Arithmetic

FINITE FIELD ARITHMETIC

In AES, all operations are performed on 8-bit bytes. In particular, the arithmetic operations of addition, multiplication, and division are performed over the finite field GF(28). Section 4.7 discusses such operations in some detail. For the reader who has not studied Chapter 4, and as a quick review for those who have, this section summarizes the important concepts.

In essence, a field is a set in which we can do addition, subtraction, multipli- cation, and division without leaving the set. Division is defined with the following rule: a/b = a(b - 1).

An example of a finite field (one with a finite number of ele- ments) is the set Zp consisting of all the integers {0, 1, ... , p - 1}, where p is a prime number and in which arithmetic is carried out modulo p.

Virtually all encryption algorithms, both conventional and public-key, involve arithmetic operations on integers. If one of the operations used in the algorithm is division, then we need to work in arithmetic defined over a field; this is because divi- sion requires that each nonzero element have a multiplicative inverse. For conve- nience and for implementation efficiency, we would also like to work with integers that fit exactly into a given number of bits, with no wasted bit patterns. That is, we wish to work with integers in the range 0 through 2n - 1, which fit into an n-bit word. Unfortunately, the set of such integers, Z2n, using modular arithmetic, is not a field. For example, the integer 2 has no multiplicative inverse in Z2n, that is, there is no integer b, such that 2b mod 2n = 1.

There is a way of defining a finite field containing 2n elements; such a field is referred to as GF(2n). Consider the set, S, of all polynomials of degree n - 1 or less with binary coefficients. Thus, each polynomial has the  form

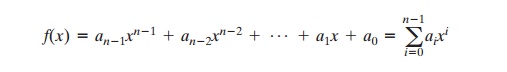
where each ai takes on the value 0 or 1. There are a total of 2n different polynomials in S. For n  = 3, the 23  = 8 polynomials in the set  are

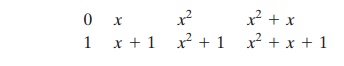
With the appropriate definition of arithmetic operations, each such set S is a finite field. The definition consists of the following elements.

1.                                                 Arithmetic follows the ordinary rules of polynomial arithmetic using the basic rules of algebra with the following two refinements.

2.                                                 Arithmetic on the coefficients is performed modulo 2. This is the same as the XOR  operation.

3.                                                 If multiplication results in a polynomial of degree greater than n - 1, then the polynomial is reduced modulo some irreducible polynomial m(x) of degree n. That is, we divide by m(x) and keep the remainder. For a polynomial f(x), the remainder is expressed as r(x) = f(x) mod m(x). A polynomial m(x) is called irreducible if and only if m(x) cannot be expressed as a product of two poly- nomials, both of degree lower than that of m(x).

For example, to construct the finite field GF(23), we need to choose an irre- ducible polynomial of degree 3. There are only two such polynomials: (x3 + x2 + 1) and  (x3  +  x  +  1). Addition is equivalent to taking the XOR of like terms. Thus,    (x  + 1)  + x  = 1.

A polynomial in GF(2n) can be uniquely represented by its n binary coeffi- cients (an - 1an - 2 ... a0). Therefore, every polynomial in GF(2n) can be represented by an n-bit number. Addition is performed by taking the bitwise XOR of the two n-bit elements. There is no simple XOR operation that will accomplish multiplication in GF(2n). However, a reasonably straightforward, easily implemented, technique is available. In essence, it can be shown that multiplication of a number in GF(2n) by 2 consists of a left shift followed by a conditional XOR with a constant. Multiplication by larger numbers can be achieved by repeated application of this rule.

To summarize, AES operates on 8-bit bytes. Addition of two bytes is defined as the bitwise XOR operation. Multiplication of two bytes is defined as multiplication   in the finite field GF(28), with the irreducible polynomial2 m(x)  =  x8  +  x4  +  x3 +  x  +     1. The developers of Rijndael give as their motivation for selecting this one of the 30 possible irreducible polynomials of degree 8 that it is the first one on the list given in [LIDL94].