Advanced Encryption Standard(AES) Transformation Functions

AES TRANSFORMATION FUNCTIONS

We now turn to a discussion of each of the four transformations used in AES. For each stage, we describe the forward (encryption) algorithm, the inverse (decryption) algorithm, and the rationale for the stage.

Substitute Bytes Transformation

FORWARD AND INVERSE TRANSFORMATIONS The forward substitute byte transformation, called SubBytes, is a  simple table lookup (Figure    5.5a). AES defines a 16 * 16 matrix of byte values, called an S-box    (Table  5.2a), that contains a permutation of all possible 256 8-bit values. Each individual byte of State is mapped into a new byte in the following way: The leftmost 4 bits of the byte are used as a row value and the rightmost 4 bits are used as a column value. These row and column values serve as indexes into the S-box to select a unique 8-bit output value. For example, the hexadecimal value3 {95} references row 9, column 5

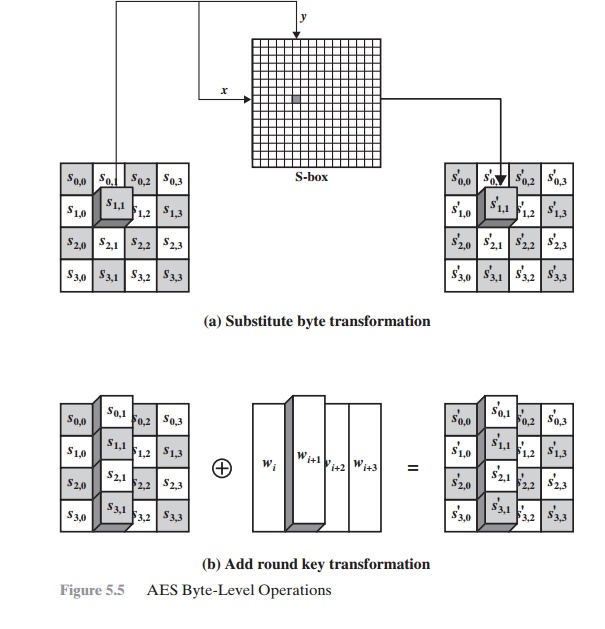
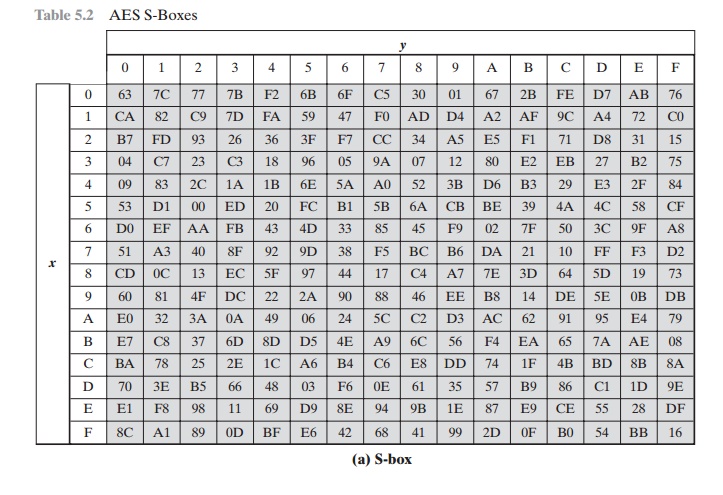
of the S-box, which contains the value {2A}. Accordingly, the value {95} is mapped into the value {2A}.

Here is an example of the SubBytes transformation:

The S-box is constructed in the following fashion (Figure 5.6a). 

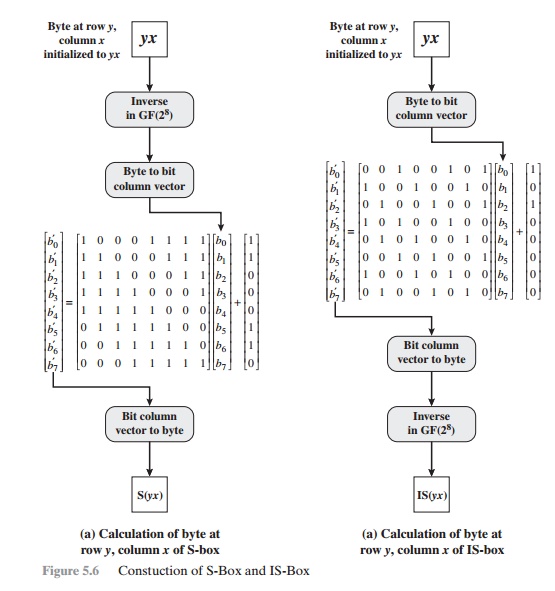
1.                                                 Initialize the S-box with the byte values in ascending sequence row by  row.

The  first row contains {00}, {01}, {02}, ... , {0F}; the second row    contains

{10}, {11}, etc.; and so on. Thus, the value of the byte at row y, column x is {yx}.

2.                                                 Map each byte in the S-box to its multiplicative inverse in the finite field GF(28); the value {00} is mapped to itself.

3.                                                 Consider that each byte in the S-box consists of 8 bits labeled (b7, b6, b5, b4, b3, b2, b1, b0). Apply the following transformation to each bit of each byte in the S-box:

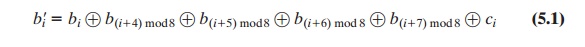
where ci is the ith bit of byte c with the value {63}; that is, (c7c6c5c4c3c2c1c0) = (01100011). The prime (¿) indicates that the variable is to be updated by the value on the right. The AES standard depicts this transformation in matrix form   as follows.

Equation (5.2) has to be interpreted carefully. In ordinary matrix multiplica- tion,4 each element in the product matrix is the sum of products of the elements of one row and one column. In this case, each element in the product matrix is the bitwise XOR of products of elements of one row and one column. Furthermore, the final addition shown in Equation (5.2) is a bitwise XOR. Recall from Section 4.7 that the bitwise XOR is addition in GF(28).

As an example, consider the input value {95}. The multiplicative inverse in GF(28) is {95} - 1 = {8A}, which is 10001010 in binary. Using Equation (5.2),

The result is {2A}, which should appear in row {09} column {05} of the S-box.

This is verified by checking Table 5.2a.

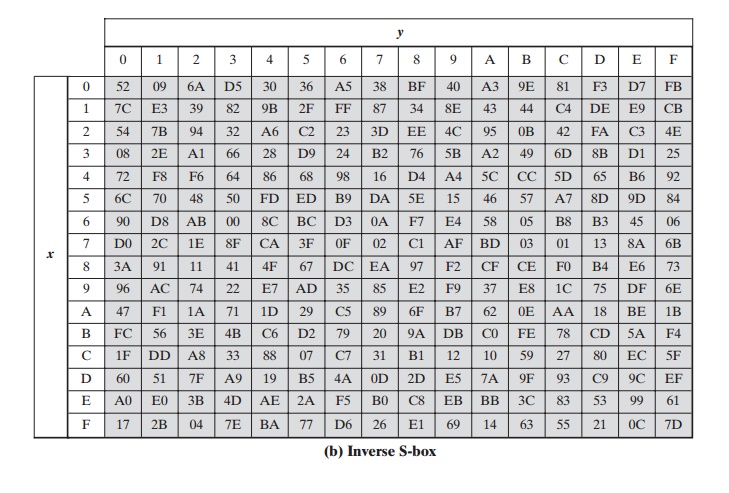
The inverse substitute byte transformation, called InvSubBytes, makes use of the inverse S-box shown in Table 5.2b. Note, for example, that the input {2A} produces the output {95}, and the input {95} to the S-box produces {2A}. The inverse S-box is constructed (Figure 5.6b) by applying the inverse of the transfor- mation in Equation (5.1) followed by taking the multiplicative inverse in GF(28).

The inverse transformation is

bi¿ =  b(i + 2) mod 8 Ⓧ b(i + 5) mod 8 Ⓧ b(i + 7) mod 8 Ⓧ di

where byte d = {05}, or 00000101. We can depict this transformation as follows.

To see that InvSubBytes is the inverse of SubBytes, label the matrices in SubBytes and InvSubBytes as X and B, respectively, and the vector versions of con- stants c and d as C and D, respectively. For some 8-bit  vector  B,  Equation  (5.2) becomes B¿ = XB Ⓧ C. We need to show  that  Y(XB Ⓧ C) Ⓧ D  =  B. To  multiply out, we must show YXB Ⓧ YC Ⓧ D   =  B. This    becomes

We have demonstrated that YX equals the identity matrix, and the YC = D, so that YC Ⓧ D equals the null vector.

RATIONALE The S-box is designed to be resistant to known cryptanalytic attacks. Specifically, the Rijndael developers sought a design that has a low correlation between input bits and output bits and the property that the output is not a linear mathematical function of the input [DAEM01]. The nonlinearity is due to the use   of the multiplicative inverse. In addition, the constant in Equation (5.1) was chosen so that the S-box has no fixed points [S-box(a) = a] and no “opposite fixed points” [S-box(a)  =  Bar a], where Bar a is the bitwise complement of a.

Of  course,  the  S-box  must  be  invertible,  that is, IS-box[S-box(a)]  =  a. 

However,  the  S-box  does  not  self-inverse  in  the  sense  that  it  is  not  true that S-box(a)  = IS-box(a). For  example, S-box({95})  =  {2A}, but  IS-box({95})  = {AD}.

ShiftRows Transformation

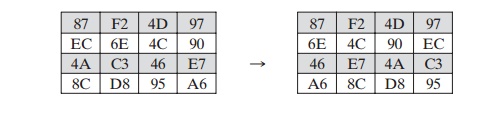
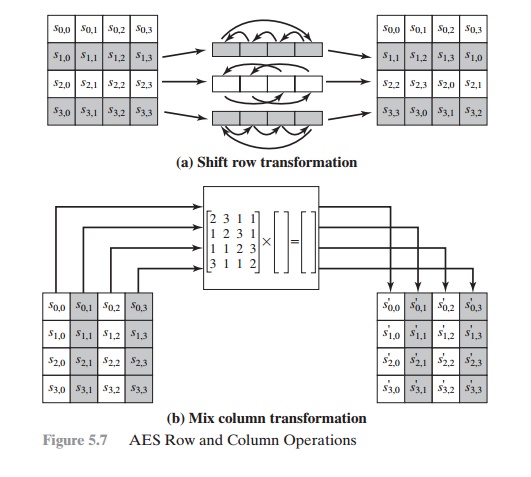
FORWARD AND INVERSE TRANSFORMATIONS The forward shift row transformation, called ShiftRows, is depicted in Figure 5.7a. The first row of State is not altered. For the second row, a 1-byte circular left shift is performed. For the third row, a 2-byte circular left shift is performed. For the fourth row, a 3-byte circular left shift is performed. The following is an example of ShiftRows.

The inverse shift row transformation, called InvShiftRows, performs the circu- lar shifts in the opposite direction for each of the last three rows, with a 1-byte circular right shift for the second row, and so on.

RATIONALE The shift row transformation is more substantial than it may first appear. This is because the State, as well as the cipher input and output, is treated as an array of four 4-byte columns. Thus, on encryption, the first 4 bytes of the plaintext are copied to the first column of State, and so on. Furthermore, as will be seen, the round key is applied to State column by column. Thus, a row shift moves an individual byte from one column to another, which is a   linear

distance of a multiple of 4 bytes. Also note that the transformation ensures that the 4 bytes of one column are spread out to four different columns. Figure 5.4 illustrates the effect.

MixColumns Transformation

FORWARD AND INVERSE TRANSFORMATIONS The forward mix column transformation, called MixColumns, operates on each column individually. Each byte of a column is mapped into a new value that is a function of all four bytes in that column. The transformation can be defined by the following matrix multiplication on State (Figure 5.7b):

Each element in the product matrix is the sum of products of elements of one row and one column. In this case, the individual additions and multiplications5 are performed in GF(28). The MixColumns transformation on a single column of State can be expressed as

Let us verify the first column of this example. Recall from Section 4.7 that, in GF(28), addition is the bitwise XOR operation and that multiplication can be per- formed according to the rule established in Equation (4.14). In particular, multipli- cation of a value by x (i.e., by {02}) can be implemented as a 1-bit left shift followed by a conditional bitwise XOR with (0001 1011) if the leftmost bit of the original value (prior to the shift) is 1. Thus, to verify the MixColumns transformation on the first column, we need to show that

The other equations can be similarly verified.

The inverse mix column transformation, called InvMixColumns, is defined by the following matrix multiplication:

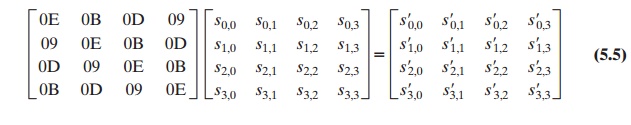
It is not immediately clear that Equation (5.5) is the inverse of Equation (5.3).

We need to show

That is, the inverse transformation matrix times the forward transformation matrix equals the identity matrix. To verify the first column of Equation (5.6), we need to show

For  the  first  equation, we  have  {0E} . {02} = 00011100  and  {09} . {03} = {09} Ⓧ ({09} # {02}) = 00001001 Ⓧ 00010010 = 00011011. Then

The other equations can be similarly verified.

The AES document describes another way of characterizing the MixColumns transformation, which is in terms of polynomial arithmetic. In the standard, MixColumns is defined by considering each column of State to be a four-term poly- nomial with coefficients in GF(28). Each column is multiplied modulo (x4 + 1) by the fixed polynomial a(x), given by

a(x) = {03}x3 + {01}x2 + {01}x + {02}    (5.7)

Appendix 5A demonstrates that multiplication of each column of State by a(x) can be written as the matrix multiplication of Equation (5.3). Similarly, it can be seen that the transformation in Equation (5.5) corresponds to treating each column as a four-term polynomial and multiplying each column by b(x), given by

b(x) = {0B}x3 + {0D}x2 + {09}x +  {0E}                  (5.8)

It readily can be shown that b(x) = a - 1(x) mod (x4 + 1).

RATIONALE The coefficients of the matrix in Equation (5.3) are based on a linear code with maximal distance between code words, which ensures a good mixing among the bytes of each column. The mix column transformation combined with the shift row transformation ensures that after a few rounds all output bits depend on all input bits. See [DAEM99] for a discussion.

In addition, the choice of coefficients in MixColumns, which are all {01}, { 02},   or { 03}, was influenced by implementation considerations. As was discussed, multi- plication by these coefficients involves at most a shift and an XOR. The  coefficients      in InvMixColumns are more formidable to implement. However, encryption  was  deemed  more  important  than  decryption  for  two   reasons:

1.                                                  For the CFB and OFB cipher modes (Figures 6.5 and 6.6; described in Chapter 6), only encryption is used.

2.                                                  As with any block cipher, AES can be used to construct a message authentica- tion code (Chapter 12), and for this, only encryption is used.

AddRoundKey Transformation

FORWARD AND INVERSE TRANSFORMATIONS In the forward add round key transfor- mation, called AddRoundKey, the 128 bits of State are bitwise XORed with the  128 bits of the round key. As shown in Figure 5.5b, the operation is viewed as a columnwise operation between the 4 bytes of a State column and one word of the round key; it can also be viewed as a byte-level operation. The following is an example  of AddRoundKey:

The first matrix is State, and the second matrix is the round key.

The inverse add round key transformation is identical to the forward add round key transformation, because the XOR operation is its own inverse.

RATIONALE The add round key transformation is as simple as possible and affects every bit of State. The complexity of the round key expansion, plus the complexity of the other stages of AES, ensure security.

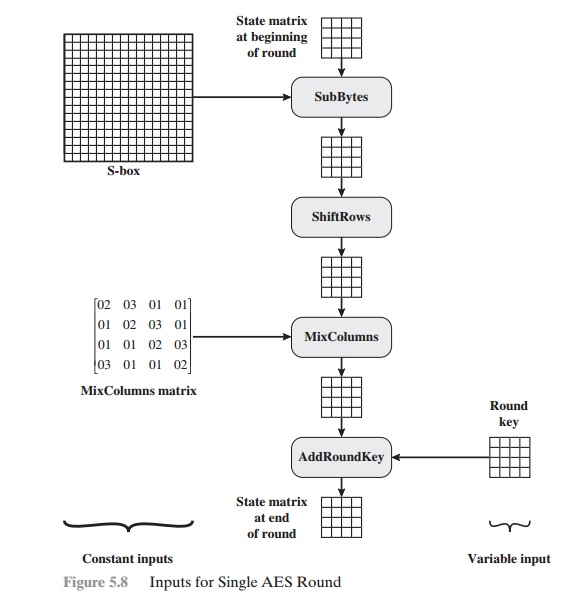
Figure 5.8 is another view of a single round of AES, emphasizing the mecha- nisms and inputs of each transformation.