AES(Advanced Encryption Standard) Structure

AES STRUCTURE

General Structure

Figure 5.1 shows the overall structure of the AES encryption process. The cipher takes a plaintext block size of 128 bits, or 16 bytes. The key length can be 16, 24, or 32 bytes (128, 192, or 256 bits). The algorithm is referred to as AES-128, AES-192, or AES-256, depending on the key length.

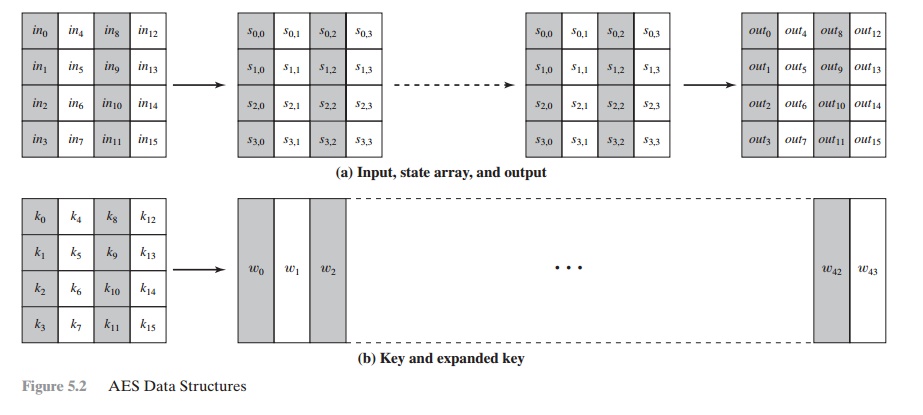
The input to the encryption and decryption algorithms is a single 128-bit block. In FIPS PUB 197, this block is depicted as a 4 * 4 square matrix of bytes. This block is copied into the State array, which is modified at each stage of encryption or decryp- tion. After the final stage, State is copied to an output matrix. These operations are depicted in Figure 5.2a. Similarly, the key is depicted as a square matrix of bytes. This key is then expanded into an array of key schedule words. Figure 5.2b shows the expansion for the 128-bit key. Each word is four bytes, and the total key schedule is 44 words for the 128-bit key. Note that the ordering of bytes within a matrix is by col- umn. So, for example, the first four bytes of a 128-bit plaintext input to the encryption cipher occupy the first column of the in matrix, the second four bytes occupy the second column, and so on. Similarly, the first four bytes of the expanded key, which form a word, occupy the first column of the w matrix.

The cipher consists of N rounds, where the number of rounds depends on the key length: 10 rounds for a 16-byte key, 12 rounds for a 24-byte key, and 14 rounds for a 32-byte key (Table 5.1). The first N - 1 rounds consist of four distinct trans- formation functions: SubBytes, ShiftRows, MixColumns, and AddRoundKey, which are described subsequently. The final round contains only three transformations, and there is a initial single transformation (AddRoundKey) before the first round,

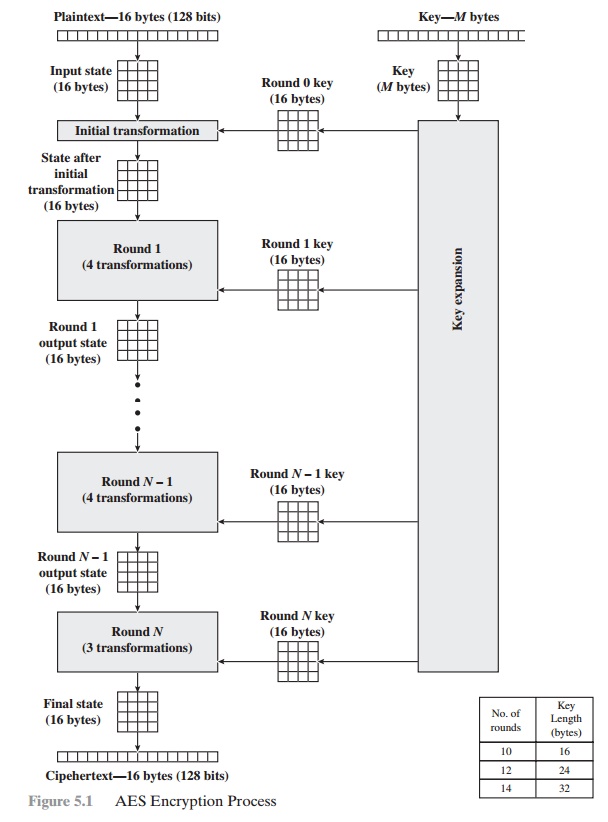
which can be considered Round 0. Each transformation takes one or more 4 * 4 matrices as input and produces a 4 * 4 matrix as output. Figure 5.1 shows that the output of each round is a 4 * 4 matrix, with the output of the final round being the ciphertext. Also, the key expansion function generates N + 1 round keys, each of which is a distinct 4 * 4 matrix. Each round key serve as one of the inputs to the AddRoundKey transformation in each round.

Detailed Structure

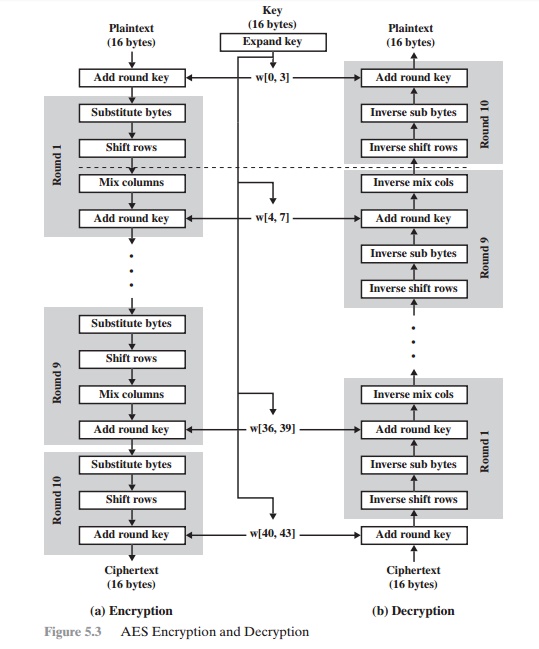
Figure 5.3 shows the AES cipher in more detail, indicating the sequence of transfor- mations in each round and showing the corresponding decryption function. As was done in Chapter 3, we show encryption proceeding down the page and decryption proceeding up the page.

Before delving into details, we can make several comments about the overall AES structure.

1.                                                 One noteworthy feature of this structure is that it is not a Feistel structure. Recall that, in the classic Feistel structure, half of the data block is used to modify the other half of the data block and then the halves are swapped. AES instead processes the entire data block as a single matrix during each round using substitutions and permutation.

2.                                                 The key that is provided as input is expanded into an array of forty-four 32-bit words, w[i]. Four distinct words (128 bits) serve as a round key for each round; these are indicated in Figure 5.3.

3.                                                 Four different stages are used, one of permutation and three of substitution:

•                       Substitute bytes: Uses an S-box to perform a byte-by-byte substitution of the block

•                       ShiftRows: A simple permutation

•                       MixColumns: A substitution that makes use of arithmetic over GF(28)

•                       AddRoundKey: A simple bitwise XOR of the current block with a portion of the expanded key

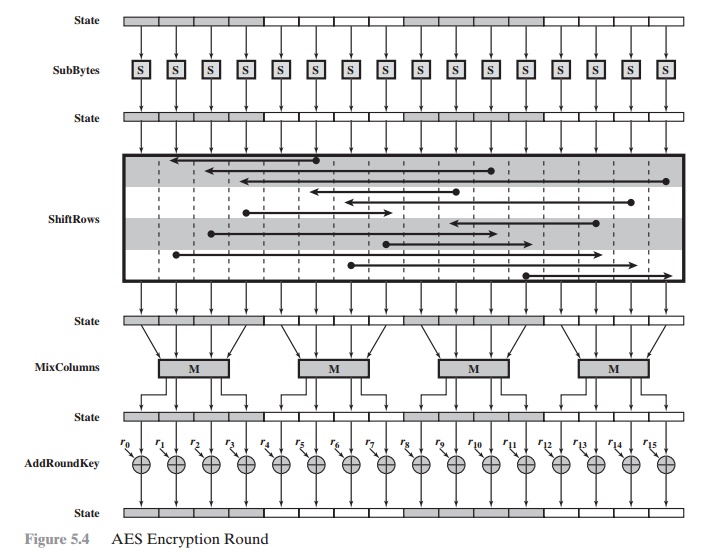
4.                                                 The structure is quite simple. For both encryption and decryption, the cipher begins with an AddRoundKey stage, followed by nine rounds that each includes all four stages, followed by a tenth round of three stages. Figure 5.4 depicts the structure of a full encryption round.

5.                                                 Only the AddRoundKey stage makes use of the key. For this reason, the cipher begins and ends with an AddRoundKey stage. Any other stage, applied at the beginning or end, is reversible without knowledge of the key and so would add no security.

6.                                                 The AddRoundKey stage is, in effect, a form of Vernam cipher and by itself would not be formidable. The other three stages together provide confusion, diffusion, and nonlinearity, but by themselves would provide no security because they do not use the key.We can view the cipher as alternating operations of XOR

encryption (AddRoundKey) of a block, followed by scrambling of the block (the other three stages), followed by XOR encryption, and so on. This scheme is both efficient and highly secure.

7.                                                                               Each stage is easily reversible. For the Substitute Byte, ShiftRows, and MixColumns stages, an inverse function is used in the decryption algorithm. For the AddRoundKey stage, the inverse is achieved by XORing the same round key to the block, using the result that A  Ⓧ B  Ⓧ B = A.

8.                                                                               As with most block ciphers, the decryption algorithm makes use of the expanded key in reverse order. However, the decryption algorithm is   not

identical to the encryption algorithm. This is a consequence of the particular structure of AES.

9.                                                                               Once it is established that all four stages are reversible, it is easy to verify that decryption does recover the plaintext. Figure 5.3 lays out encryption and decryption going in opposite vertical directions. At each horizontal point (e.g., the dashed line in the figure), State is the same for both encryption and decryption.

10.                                                                         The final round of both encryption and decryption consists of only three stages. Again, this is a consequence of the particular structure of AES and is required to make the cipher reversible.