AES(Advanced Encryption Standard) Implementation

AES IMPLEMENTATION

Equivalent Inverse Cipher

As was mentioned, the AES decryption cipher is not identical to the encryption cipher (Figure 5.3). That is, the sequence of transformations for decryption differs from that for encryption, although the form of the key schedules for encryption and decryption is the same. This has the disadvantage that two separate software or firmware modules are needed for applications that require both encryption and decryption. There is, however, an equivalent version of the decryption algorithm that has the same structure as the encryption algorithm. The equivalent version has the same sequence of transformations as the encryption algorithm (with transfor- mations replaced by their inverses). To achieve this equivalence, a change in key schedule is needed.

Two separate changes are needed to bring the decryption structure in line with the encryption structure. As illustrated in Figure 5.3, an encryption round has the structure SubBytes, ShiftRows, MixColumns, AddRoundKey. The standard decryption round has the structure InvShiftRows, InvSubBytes, AddRoundKey, InvMixColumns. Thus, the first two stages of the decryption round need to  be interchanged, and the second two stages of the decryption round need to be interchanged.

INTERCHANGING INVSHIFTROWS AND INVSUBBYTES InvShiftRows affects the sequence of bytes in State but does not alter byte contents and does not depend on byte contents to perform its transformation. InvSubBytes affects the contents of bytes in State but does not alter byte sequence and does not depend on byte sequence  to perform its transformation. Thus, these two operations commute and can be interchanged. For a given State Si,

InvShiftRows  [InvSubBytes  (Si)]  =  InvSubBytes [InvShiftRows (Si)]

INTERCHANGING ADDROUNDKEY AND INVMIXCOLUMNS The transformations Add- RoundKey and InvMixColumns do not alter the sequence of bytes in State. If we view the key as a sequence of words, then both AddRoundKey and InvMixColumns operate on State one column at a time. These two operations are linear with respect to the column input. That is, for a given State Si and a given round key wj,

InvMixColumns  (Si Ⓧ wj)  =  [InvMixColumns (Si)] Ⓧ [InvMixColumns (wj)]

To  see  this, suppose  that  the  first  column  of  State Si is  the sequence is  the sequence (y0, y1, y2, y3) and the first column of the round key wj is (k0, k1, k2, k3). Then we need to show

This equation is valid by inspection.Thus, we can interchange AddRoundKey and InvMixColumns, provided that we first apply InvMixColumns to the round key. Note that we do not need to apply InvMixColumns to the round key for the input to the first AddRoundKey transformation (preceding the first round) nor to the last AddRoundKey transformation (in round 10).This is because these two AddRoundKey transformations are not interchanged with InvMixColumns to produce the equivalent decryption algorithm.

Figure 5.10 illustrates the equivalent decryption algorithm.

Implementation Aspects

The Rijndael proposal [DAEM99] provides some suggestions for efficient imple- mentation on 8-bit processors, typical for current smart cards, and on 32-bit proces- sors, typical for PCs.

8-BIT PROCESSOR AES can be implemented very efficiently on an 8-bit processor. AddRoundKey is a bytewise XOR operation. ShiftRows is a simple byte-shifting operation. SubBytes operates at the byte level and only requires a table of 256 bytes. The transformation MixColumns requires matrix multiplication in the field GF(28), which means that all operations are carried out on bytes.

The transformation MixColumns requires matrix multiplication in the field GF(28), which means that all operations are carried out on bytes. MixColumns only requires multiplication by {02} and {03}, which, as we have seen, involved simple shifts, conditional XORs, and XORs. This can be implemented in a more efficient way that eliminates the shifts and conditional XORs. Equation set (5.4) shows the equations for the MixColumns transformation on a single column. Using the identity {03}  x = ({02}  x) Ⓧ x, we can rewrite Equation set (5.4) as  follows.

The multiplication by {02} involves a shift and a conditional XOR. Such an imple- mentation may be vulnerable to a timing attack of the sort described in Section 3.4. To counter this attack and to increase processing efficiency at the cost of some storage, the multiplication can be replaced by a table lookup. Define the 256-byte table X2, such that X2[i] = {02}  i. Then Equation set (5.9) can be rewritten as

32-BIT PROCESSOR The implementation described in the preceding subsection uses only 8-bit operations. For a 32-bit processor, a more efficient implementation can be achieved if operations are defined on 32-bit words. To show this, we first define the four transformations of a round in algebraic form. Suppose we begin with a State matrix consisting of elements ai, j and a round-key matrix consisting of elements ki, j. Then the transformations can be expressed as follows.

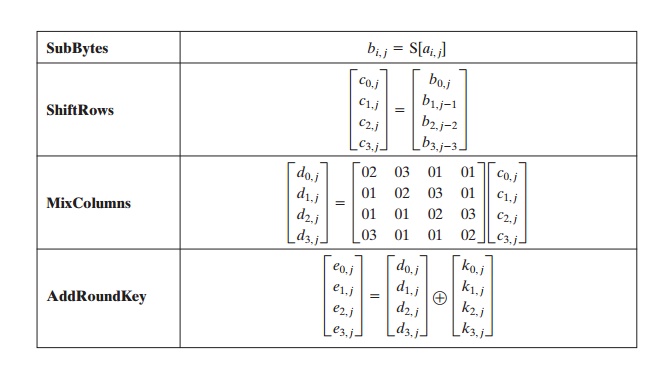
In the ShiftRows equation, the column indices are taken mod 4. We can com- bine all of these expressions into a single equation:

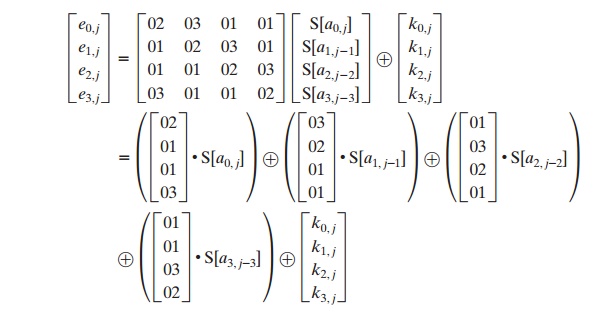
In the second equation, we are expressing the matrix multiplication as a linear com- bination of vectors. We define four 256-word (1024-byte) tables as follows.

Thus, each table takes as input a byte value and produces a column vector (a 32-bit word) that is a function of the S-box entry for that byte value. These tables can be calculated in advance.

We can define a round function operating on a column in the following fashion.

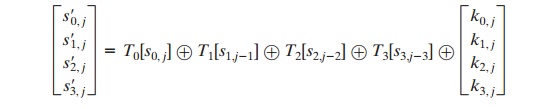
As a result, an implementation based on the preceding equation requires only four table lookups and four XORs per column per round, plus 4 Kbytes to store the table. The developers of Rijndael believe that this compact, efficient implementation was probably one of the most important factors in the selection of Rijndael for AES.