An Advanced Encryption Standard(AES) Example

AN AES EXAMPLE

We now work through an example and consider some of its implications. Although you are not expected to duplicate the example by hand, you will find it informative   to study the hex patterns that occur from one step to the next.

For this example, the plaintext is a hexadecimal palindrome. The plaintext, key, and resulting ciphertext are

Plaintext:    0123456789abcdeffedcba9876543210

Key:  0f1571c947d9e8590cb7add6af7f6798

Ciphertext: ff0b844a0853bf7c6934ab4364148fb9

Results

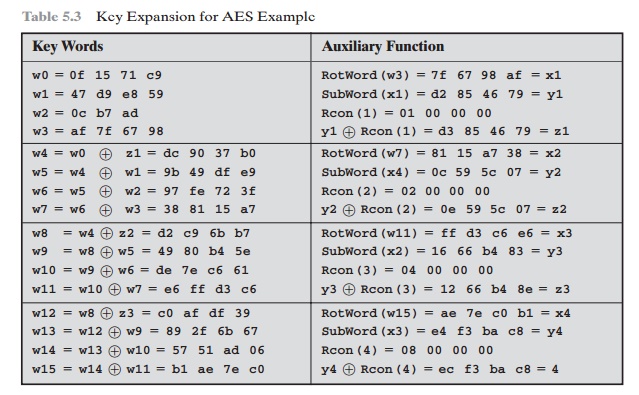
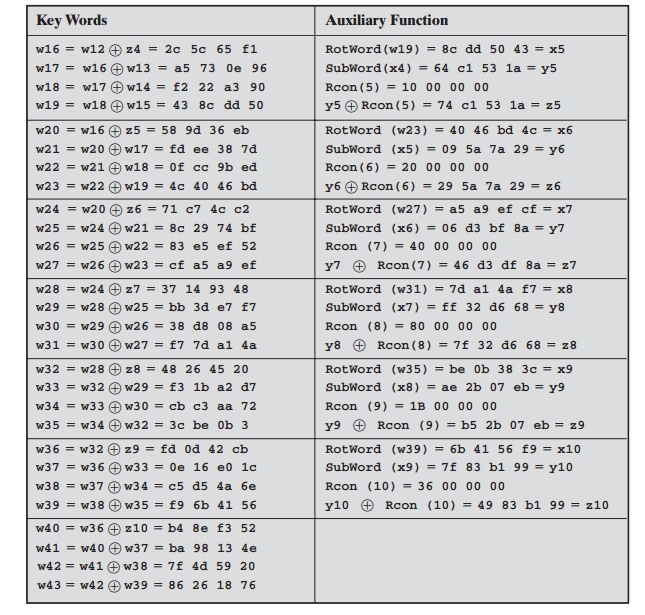
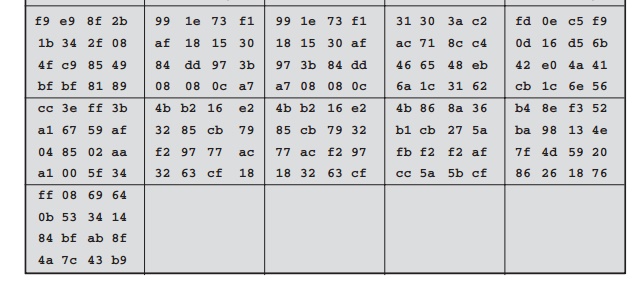
Table 5.3 shows the expansion of the 16-byte key into 10 round keys. As previously explained, this process is performed word by word, with each four-byte word occupy- ing one column of the word round-key matrix. The left-hand column shows the four round-key words generated for each round. The right-hand column shows the steps

Table 5.3  Key Expansion for AES Example

used to generate the auxiliary word used in key expansion. We begin, of course, with the key itself serving as the round key for round 0.

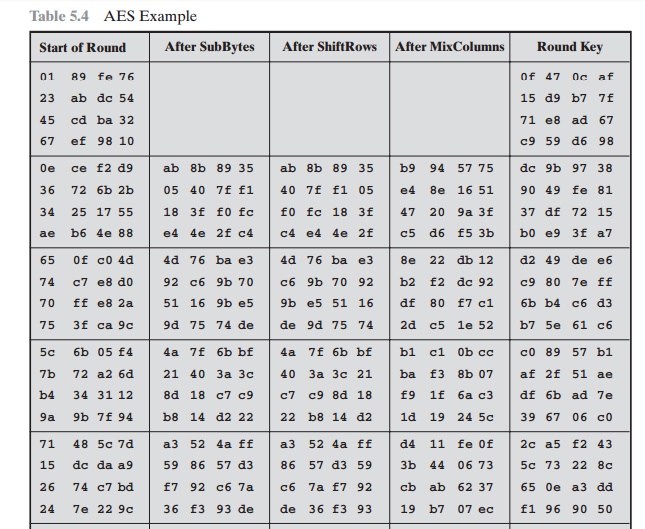
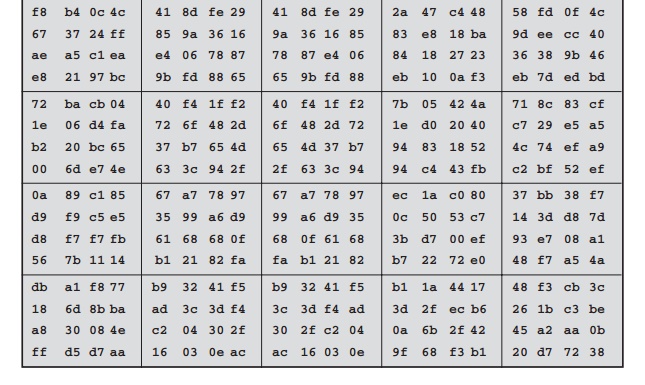
Next, Table 5.4 shows the progression of State through the AES encryption process. The first column shows the value of State at the start of a round. For the first row, State is just the matrix arrangement of the plaintext.The second, third, and fourth columns show the value of State for that round after the SubBytes, ShiftRows, and MixColumns transformations, respectively. The fifth column shows the round key. You can verify that these round keys equate with those shown in Table 5.3. The first column shows the value of State resulting from the bitwise XOR of State after the preceding MixColumns with the round key for the preceding round.

Avalanche Effect

If a small change in the key or plaintext were to produce a corresponding small change in the ciphertext, this might be used to effectively reduce the size of the

plaintext (or key) space to be searched. What is desired is the avalanche effect, in which a small change in plaintext or key produces a large change in the ciphertext.

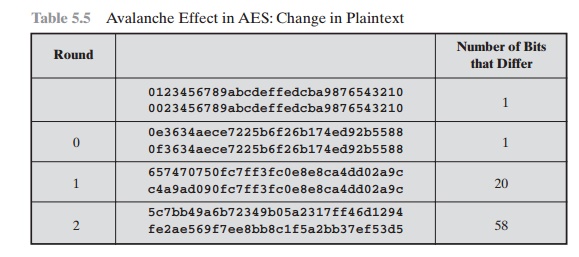
Using the example from Table 5.4, Table 5.5 shows the result when the eighth bit of the plaintext is changed. The second column of the table shows the value of the State matrix at the end of each round for the two plaintexts. Note that after just one round, 20 bits of the State vector differ. After two rounds, close to half the bits differ. This magnitude of difference propagates through the remaining rounds. A bit difference in approximately half the positions in the most desirable outcome. Clearly, if almost all the bits are changed, this would be logically equivalent to almost none of the bits being changed. Put another way, if we select two plaintexts at random, we would expect the two plaintexts to differ in about half of the bit positions and the two ciphertexts to also differ in about half the positions.

Table 5.6 shows the change in State matrix values when the same plaintext    is used and the two keys differ in the eighth bit. That is, for the second case, the   key is 0e1571c947d9e8590cb7add6af7f6798. Again, one round produces a

Table 5.5  Avalanche Effect in AES: Change in Plaintext

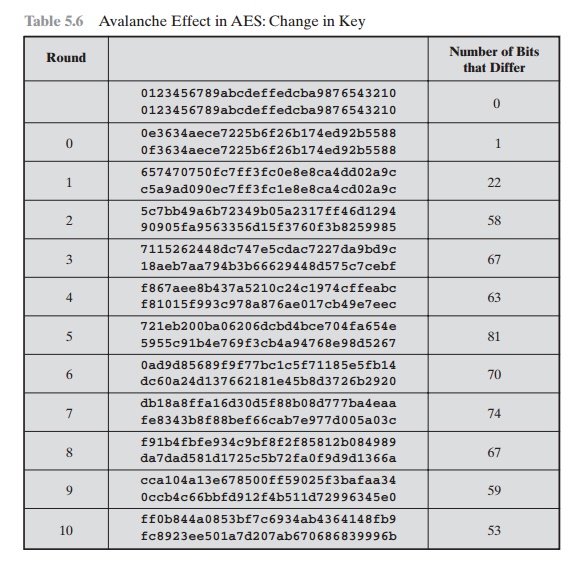
significant change, and the magnitude of change after all subsequent rounds is roughly half the bits. Thus, based on this example, AES exhibits a very strong avalanche effect.

Note that this avalanche effect is stronger than that for DES (Table 3.5), which requires three rounds to reach a  point at  which approximately half  the bits are changed, both for a bit change in the plaintext and a bit change in the key.