AES Key Expansion

AES KEY EXPANSION

Key Expansion Algorithm

The AES key expansion algorithm takes as input a four-word (16-byte) key and produces a linear array of 44 words (176 bytes). This is sufficient to provide a four-word round key for the initial AddRoundKey stage and each of the 10 rounds of the cipher. The pseudocode on the next page describes the expansion.

The key is copied into the first four words of the expanded key. The remain- der of the expanded key is filled in four words at a time. Each added word w[i] depends on the immediately preceding word, w[i  - 1], and the word four posi-  tions back, w[i - 4]. In three out of four cases, a simple XOR is used. For a word whose position in the w array is a multiple of 4, a more complex function is used. Figure 5.9 illustrates the generation of the expanded key, using the symbol g to represent that complex function. The function g consists of the following subfunctions.

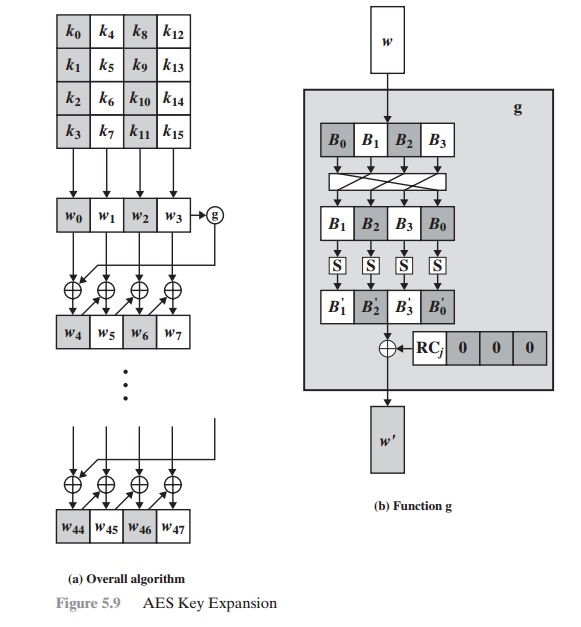
1.         RotWord performs a one-byte circular left shift on a word. This means that an input word [B0, B1, B2, B3] is transformed into [B1, B2, B3, B0].

2.         SubWord performs a byte substitution on each byte of its input word, using the S-box (Table 5.2a).

3.         The result of steps 1 and 2 is XORed with a round constant, Rcon[j].

The round constant is a word in which the three rightmost bytes are always 0. Thus, the effect of an XOR of a word with Rcon is to only perform an XOR on the left- most byte of the word. The round constant is different for each round and is defined as Rcon[j] = (RC[j], 0, 0, 0), with RC[1] = 1, RC[j] = 2 RC[j -1] and with multiplica- tion defined over the field GF(28). The values of RC[j] in hexadecimal are

For example, suppose that the round key for round 8 is

EA D2 73 21 B5 8D BA D2 31 2B F5 60 7F 8D 29 2F

Then the first 4 bytes (first column) of the round key for round 9 are calculated as follows:

Rationale

The Rijndael developers designed the expansion key algorithm to be resistant to known cryptanalytic attacks. The inclusion of a round-dependent round constant eliminates the symmetry, or similarity, between the ways in which round keys are generated in different rounds. The specific criteria that were used are [DAEM99]

•                           Knowledge of a part of the cipher key or round key does not enable calcula- tion of many other round-key bits.

•                           An invertible transformation [i.e., knowledge of any Nk consecutive words of the expanded key enables regeneration the entire expanded key (Nk = key size in words)].

•                           Speed on a wide range of processors.

•                           Usage of round constants to eliminate symmetries.

•                           Diffusion of cipher key differences into the round keys; that is, each key bit affects many round key bits.

•                           Enough nonlinearity to prohibit the full determination of round key differ- ences from cipher key differences only.

•                           Simplicity of description.

The authors do not quantify the first point on the preceding list, but the idea is that if you know less than Nk consecutive words of either the cipher key or one of the round keys, then it is difficult to reconstruct the remaining unknown bits. The fewer bits one knows, the more difficult it is to do the reconstruction or to determine other bits in the key expansion.