Fiber cutoff wavelength measurements

Fiber cutoff wavelength measurements

A multimode fiber has many cutoff wavelengths because the number of bound propagating modes is usually large. For example, considering a parabolic refractive index graded fiber, the number of guided modes Mg is:

where a is the core radius and n1 and n2 are the core peak and cladding indices respectively. It may be observed from Eq. (4.14) that operation at longer wavelengths yields fewer guided modes. Therefore it is clear that as the wavelength is increased, a growing number of modes are cutoff where the cutoff wavelength of aLPlm mode is the maximum wavelength for which the mode is guided by the fiber.

Usually the cutoff wavelength refers to the operation of single-mode fiber in that it is the cutoff wavelength of the LP11 mode (which has the longest cutoff wavelength) which makes the fiber single moded when the fiber diameter is reduced to 8 or 9 μm. Hence the cutoff wavelength of the LP11 is the shortest wavelength above which the fiber exhibits single-mode operation and it is therefore an important parameter to measure.

The theoretical value of the cutoff wavelength can be determined from the fiber refractive index profile. Because of the large attenuation of the LP11 mode near cutoff, however, the parameter which is experimentally determined is called the effective cutoff wavelength, which is always smaller than the theoretical cutoff wavelength by as much as 100 to 200 nm. It is this effective cutoff wavelength which limits the wavelength region for which the fiber is ‘effectively’ single-mode.

 In the bending-reference technique the power Ps(λ) transmitted through the fiber sample in the configurations shown in Figure 4.16 is measured as a function of wavelength. Thus the quantity Ps(λ) corresponds to the total power, including launched higher order modes, of the ITU-T definition for cutoff wavelength. Then keeping the launch conditions fixed, at least one additional loop of sufficiently small radius (60 mm or less) is introduced into the test sample to act as a mode filter to suppress the secondary LP11 mode without attenuating the fundamental mode at the effective cutoff wavelength. In this case the smaller transmitted spectral power Pb(λ) is measured which corresponds to the fundamental mode power referred to in the definition. The bend attenuation ab(λ) comprising the level difference between the total power and the fundamental power is calculated as:

The bend attenuation characteristic exhibits a peak in the wavelength region where the radiation losses resulting from the small loop are much higher for the LP11 mode than for the LP01 fundamental mode, as illustrated in Figure 4.17.

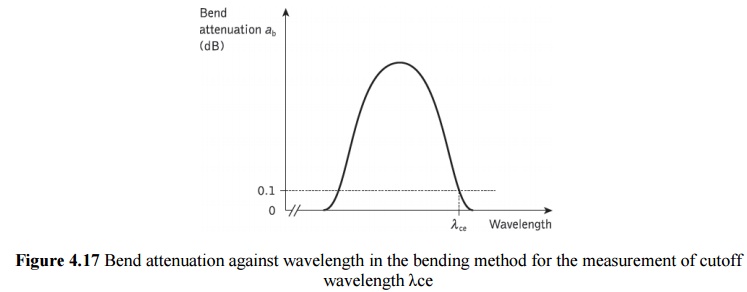
It should be noted that the shorter wavelength side of the attenuation maximum corresponds to the LP11 mode, being well confined in the fiber core, and hence negligible loss is induced by the 60 mm diameter loop, whereas on the longer wavelength side the LP11 mode is not guided in the fiber and therefore, assuming that the loop diameter is large enough to avoid any curvature loss to the fundamental mode, there is also no increase in loss.

The relative attenuation am(λ) or level difference between the powers launched into the multimode and single-mode fibers may be computed as: