Evaluating Quality Assurance Data: Performance-Based Approach

Performance-Based Approach

In a performance-based approach to quality assurance, a laboratory is free to use its experience to determine the best way to gather and monitor quality assessment data. The quality assessment methods remain the same (duplicate samples, blanks, standards, and spike recoveries) since they provide the necessary information about precision and bias. What the laboratory can control, however, is the fre- quency with which quality assessment samples are analyzed, and the conditions in- dicating when an analytical system is no longer in a state of statistical control. Fur- thermore, a performance-based approach to quality assessment allows a laboratory to determine if an analytical system is in danger of drifting out of statistical con- trol. Corrective measures are then taken before further problems develop.

The principal tool for performance-based quality assessment is the control chart. In a control chart the results from the analysis of quality assessment samples are plotted in the order in which they are collected, providing a continuous record of the statistical state of the analytical system. Quality assessment data collected over time can be summarized by a mean value and a standard deviation. The fundamen- tal assumption behind the use of a control chart is that quality assessment data will show only random variations around the mean value when the analytical system is in statistical control. When an analytical system moves out of statistical control, the quality assessment data is influenced by additional sources of error, increasing the standard deviation or changing the mean value.

Control charts were originally developed in the 1920s as a quality assurance tool for the control of manufactured products.11 Two types of control charts are commonly used in quality assurance: a property control chart in which results for single measurements, or the means for several replicate measurements, are plotted sequentially; and a precision control chart in which ranges or standard deviations are plotted sequentially. In either case, the control chart consists of a line represent- ing the mean value for the measured property or the precision, and two or more boundary lines whose positions are determined by the precision of the measure- ment process. The position of the data points about the boundary lines determines whether the system is in statistical control.

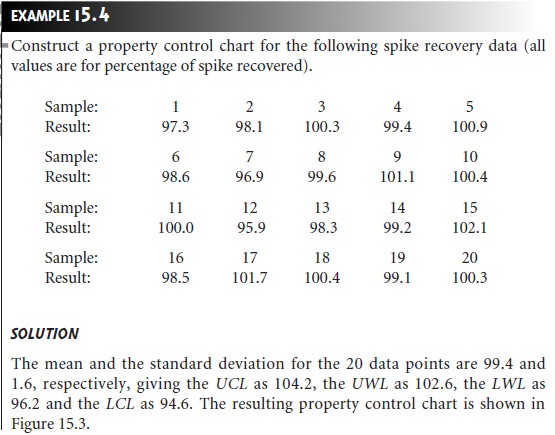
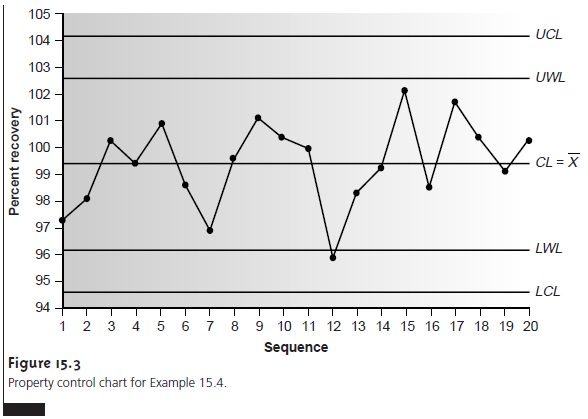
Construction of Property Control Charts 

The simplest form for a property control chart is a sequence of points, each of which represents a single determination of the property being monitored. To construct the control chart, it is first necessary to de- termine the mean value of the property and the standard deviation for its measure- ment. These statistical values are determined using a minimum of 7 to 15 samples (although 30 or more samples are desirable), obtained while the system is known to be under statistical control. The center line (CL) of the control chart is determined by the average of these n points

The positions of the boundary lines are determined by the standard deviation, S, of the points used to determine the central line

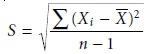
with the upper and lower warning limits (UWL and LWL), and the upper and lower control limits (UCL and LCL) given by

Property control charts can also be constructed using points that are the mean value, X–_i, for a set of r replicate determinations on a single sample. The mean for the ith sample is given by

where X_ij is the jth replicate. The center line for the control chart, therefore, is

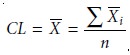
To determine the standard deviation for the warning and control limits, it is neces- sary to calculate the variance for each sample, s _i ².

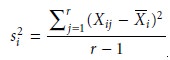
The overall standard deviation, S, is the square root of the average variance for the samples used to establish the control plot.

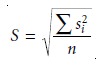
Finally, the resulting warning and control limits are

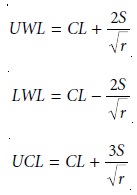
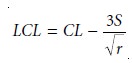
Constructing a Precision Control Chart 

The most common measure of precision used in constructing a precision control chart is the range, R, between the largest and smallest results for a set of j replicate analyses on a sample.

R = X_large – X_small

To construct the control chart, ranges for a minimum of 15–20 samples (prefer- ably 30 or more samples) are obtained while the system is known to be in statistical control. The line for the average range, R’ , is determined by the mean of thesen samples

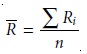
The upper control line and the upper warning line are given by

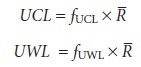
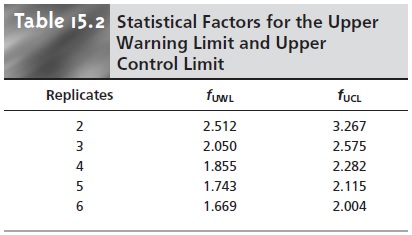
where f_UCL and f_UWL (Table 15.2) are statistical factors determined by the number of replicates used to determine the range. Because the range always is greater than or equal to zero, there is no lower control limit or lower warning limit.

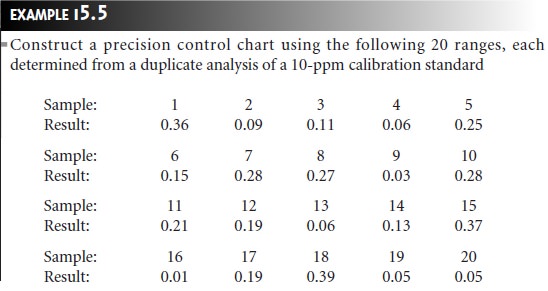
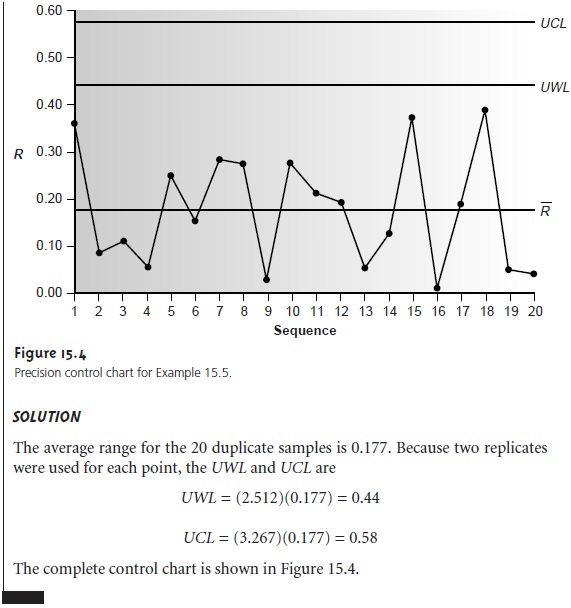
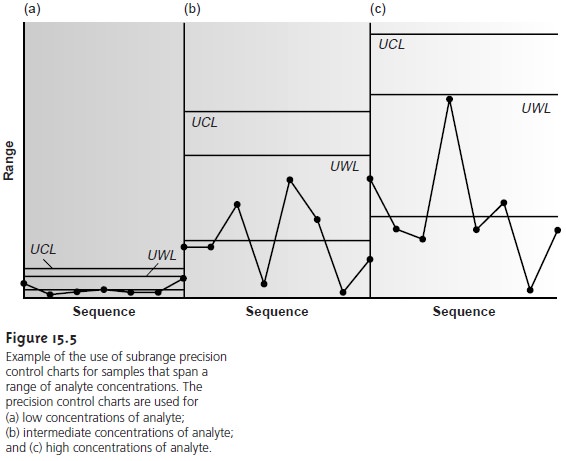
The precision control chart is strictly valid only for the replicate analysis of identical samples, such as a calibration standard or a standard reference material. Its use for the analysis of nonidentical samples, such as a series of clinical or environ- mental samples, is complicated by the fact that the range usually is not independent of the magnitude of X_large and X_small. For example, Table 15.3 shows the relationship10 between R and the concentration of chromium in water. Clearly the significant difference in the average range for these concentrations of Cr makes a single preci- sion control chart impossible. One solution to this problem is to prepare separateprecision control charts, each of which covers a range of concentrations for which R is approximately constant (Figure 15.5).

Interpreting Control Charts 

The purpose of a control chart is to determine if a sys- tem is in statistical control. This determination is made by examining the location of individual points in relation to the warning limits and the control limits, and the distribution of the points around the central line. If we assume that the data are normally distributed, then the probability of finding a point at any distance from the mean value can be determined from the normal distribution curve. The upper and lower control limits for a property control chart, for example, are set to ±3S, which, if S is a good approximation for σ, includes 99.74% of the data. The proba- bility that a point will fall outside the UCL or LCL, therefore, is only 0.26%. 

The most likely explanation when a point exceeds a control limit is that a systematic error has occurred or that the precision of the measurement process has deterio- rated. In either case the system is assumed to be out of statistical control.

Rule 1. A system is considered to be out of statistical control if any single point exceeds either the UCL or the LCL.

The upper and lower warning limits, which are located at ±2S, should only be ex- ceeded by 5% of the data; thus

Rule 2. A system is considered to be out of statistical control if two out of three consecutive points are between the UWL and UCL or between the LWL and LCL.

When a system is in statistical control, the data points should be randomly dis- tributed about the center line. The presence of an unlikely pattern in the data is an- other indication that a system is no longer in statistical control.4,12 Thus,

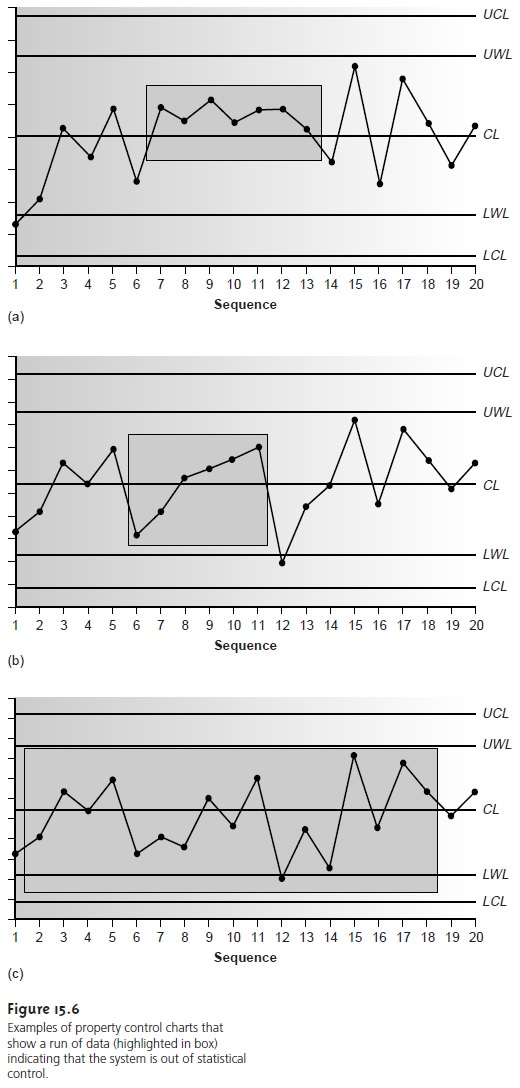
Rule 3. A system is considered to be out of statistical control if a run of seven consecutive points is completely above or completely below the center line (Figure 15.6a).

Rule 4. A system is considered to be out of statistical control if six consecutive points are all increasing in value or all decreasing in value (Figure 15.6b). The points may be on either side of the center line.

Rule 5. A system is considered to be out of statistical control if 14 consecutive points alternate up and down in value (Figure 15.6c). The points may be on either side of the center line.

Rule 6. A system is considered to be out of statistical control if any obvious “nonrandom” pattern is observed.

The same rules apply to precision control charts with the exception that there are no lower warning and lower control limits.

Using Control Charts for Quality Assurance 

Control charts play an important role in a performance-based program of quality assurance because they provide an easily interpreted picture of the statistical state of an analytical system. Quality assessment samples such as blanks, standards, and spike recoveries can be monitored with prop- erty control charts. A precision control chart can be used to monitor duplicate samples.

The first step in using a control chart for quality assurance is to determine the mean value and the standard deviation (except when using the range) for the quality assessment data while the system is under statistical control. These values must be es- tablished under the same conditions that will be present during the normal use of the control chart. Thus, preliminary data should be randomly collected throughout the day, as well as over several days, to account for short-term and long-term variability. The preliminary data are used to construct an initial control chart, and discrepant points are determined using the rules discussed in the previous section. Questionable points are dropped, and the control chart is replotted. As the control chart is used, it may become apparent that the original limits need adjusting. Control limits can be re- calculated if the number of new data points is at least equivalent to the amount of data used to construct the original control chart. For example, if 15 points were initially used, the limits can be reevaluated after 15 additional points are collected. The 30 points are pooled together to calculate the new limits. A second modification can be made after a further 30 points have been collected. Another indication that a control chart needs to be modified is when points rarely exceed the warning limits. In this case the new limits can be recalculated using the last 20 points.

Once a control chart is in use, new quality assessment data should be added at a rate sufficient to ensure that the system remains in statistical control. As with prescriptive approaches to quality assurance, when a quality assessment sample is found to be out of statistical control, all samples analyzed since the last successful verification of statistical control must be reanalyzed. The advantage of a performance-based approach to quality assurance is that a laboratory may use its experience, guided by control charts, to determine the frequency for collect- ing quality assessment samples. When the system is stable, quality assessment samples can be acquired less frequently.