Chapter: Operations Research: An Introduction : Integer Linear Programming
Either Or and If Then Constraints- Integer Linear Programming Illustrative Applications
Either-Or and If-Then Constraints
In the fIxed-charge problem (Section 9.1.3), we used binary variables to
handle the discontinuity in the objective cost function. In this section, we
deal with models in which constraints are not satisfied simultaneously
(either-or) or are dependent (if-then), again using binary variables. The
transformation does not change the "or" or "dependence"
nature of the constraints. It simply uses a mathematical trick
to present them in the desired format of "and" constraints.
Example 9.1-4 (Job-Sequencing
Model)
Jobco
uses a single machine to process three jobs. Both the processing time and the
due date (in days) for each job are given in the following table. The due dates
are measured from zero, the assumed start time of the first job.

The
objective of the problem is to determine the minimum late-penalty sequence for
processing the three jobs.
Define
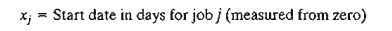
The
problem has two types of constraints: the noninterference constraints
(guaranteeing that no two jobs are processed concurrently) and the due-da te
constraints. Consider the noninterference constraints first.
Two jobs i and j with processing time pi and pj will not
be processed concurrently if either xi ≥ xj + pj or xj
≥ xi
+ pi, depending
on whether job j precedes job i, or vice
versa. Because all mathematical programs deal with simultaneous constraints only, we
transform the either-or constraints by introducing the following auxiliary
binary variable:
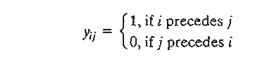
For M sufficiently large, the either-or
constraint is converted to the following two simultaneous constraints
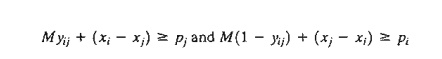
The
conversion guarantees that only one of the two constraints can be active at
anyone time. If yij = 0, the first constraint is
active, and the second is redundant (because its left-hand side will include M, which is much larger than pi). If yij = 1, the first constraint
is redundant, and the second is active.
Next, the
due-date constraint is considered. Given that dj is the due date for job j, let sj be an
unrestricted variable. Then, the associated constraint is

The
integer variables, y12, y13, and y23,
are introduced to convert the either-or constraints into simultaneous
constraints. The resulting model is a mixed
ILP.
To solve
the model, we choose M = 100, a
value that is larger than the sum of the processing times for all three
activities.
The
optimal solution is xl = 20, x2, =0, and x3 = 25,
This means that job 2 starts at time 0, job 1 starts at time 20, and job 3
starts at time 25, thus yielding the optimal processing sequence 2 -> 1 -> 3. The solution calls for completing job 2 at time 0 + 20 = 20, job 1 at time = 20 + 5 = 25, and job 3 at 25 + 15 = 40 days. Job 3 is delayed by 40
- 35 = 5 days past its due date at a cost of 5 X $34 =
$170.
AMPl Moment
File ampIEx9.1-4.txt provides the AMPL model for the problem of Example
9.1-4. The model is self-explanatory because it is a direct translation of the
general mathematical model given above. It can
handle any number of jobs by changing the input data. Note that the model is a direct
function of the raw data: processing time p, due date d, and
delay penalty perDayPenal ty.

Example 9.1-5 (Job
Sequencing Model Revisited)
In Example 9.1-4, suppose that we have the following additional
condition: If job i precedes job j then job k must precede job m.
Mathematically, this if-then condition is translated as
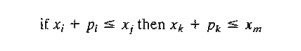
Given ε > 0 and infinitesimally small and M sufficiently large, this condition is equivalent to the following two
simultaneous constraints:
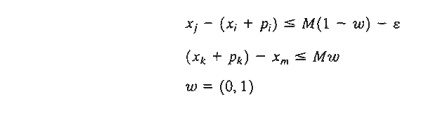
If xi + pi ≤ xj, then xj - (xi + pi) ≥ 0, which
requires w = 0, and the
second constraint be-comes xk
+ pk ≤ x m , as desired. Else, w may assume the value 0 or 1, in which case the
second constraint mayor may not be satisfied, depending on other conditions in
the model
PROBLEM SET 9.10
*1. A game board consists of nine equal squares. You are required to fill each square with a number between 1 and 9 such that
the sum of the numbers in each row, each column, and each diagonal equals 15.
Additionally, the numbers in all the squares must be distinct. Use ILP to
determine the assignment of numbers to squares.
2. A machine is used to produce two interchangeable products. The daily
capacity of the machine can produce at most 20 units of product 1 and 10 units of product 2. Alterna-tively, the machine can
be adjusted to produce at most 12 units of product 1 and 25 units of product 2 daily. Market analysis shows that the maximum daily demand for the two
products combined is 35 units. Given that the unit profits for the two
respective products are $10 and $12, which of the two machine settings should
be selected? For-mulate the problem as an ILP and find the optimum. [Note: This two-dimensional prob-lem can
be solved by inspecting the graphical solution space. This is not the case for
the n-dimensional problem.]
*3. Gapco manufactures three products, whose daily labor and raw
material requirements are given in the following table.

The profits per unit of the three products are $25, $30, and $22,
respectively. Gapco has two options for locating its plant. The two locations
differ primarily in the availability of labor and raw material, as shown in the
following table:
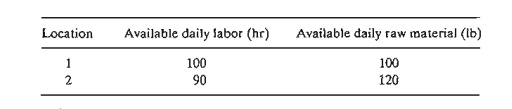
Formulate the problem as an ILP, and determine the optimum location of
the plant.
4. Jobco Shop has 10 outstanding jobs to be processed on a single machine. The
following table provides processing
times and due dates. All times are in days and due time is measured from time
0:
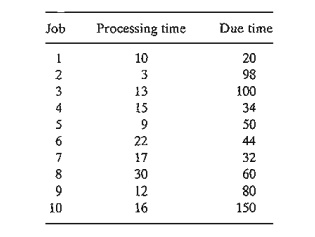
If job 4 precedes job 3, then job 9 must precede job 7. The objective is to
process a1l1O
jobs in the shortest possible time. Formulate the
model as an ILP and determine the opti-mum solution by modifying AMPL file
ampIEx9.1-4.txt.
5. In Problem 4, suppose that job 4 cannot be processed until job 3 has
been completed.
Also, machine settings for jobs 7 and 8 necessitate processing them one
right after the other (Le., job 7 immediately succeeds or immediately precedes 8). lobco's
objective is to process all ten jobs with the smal1est sum of due-time
violations. Formulate the model mathematically and determine the optimum
solution.
6.Jaco owns a plant in which three products are manufactured. The labor
and raw material requirements for the three products are given in the following
table.
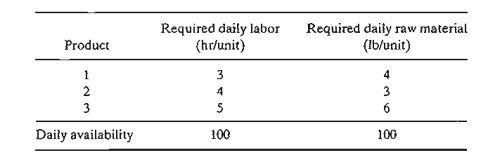
The profits per unit for the three products are $25, $30, and $45,
respectively. If product 3 is to be manufactured at all, then its production level must
be at least 5 units daily. For-mulate the problem as a mixed ILP, and find the
optimal mix.
7. UPak is a subsidiary of an LTL (Iess-than-truck-load) transportation
company. Cus-tomers bring their shipments to the UPak terminal to be loaded on
the trailer and can rent space up to 36 ft. The customer pays for the exact
linear space (in foot increments) the shipment occupies. No partial shipment is
allowed, in the sense that the entire ship-ment per customer must be on the
same trailer. A movable barrier, called bulkhead, is in-stalled to separate
different shipments. The per-foot fee UPak collects depends on the destination
of the shipment: The longer the trip, the higher the fee. The following table
provides the outstanding orders UPak needs to process.

The terminal currently has two trailers ready to be loaded. Detennine
the priority orders that will maximize the total income from the two trailers. (Hint A formulation using binary xij to represent load i on trailer j is straightforward. However, you
are challenged to define Xij as feet assigned
to load i in trailer j. The use if-then constraint to prevent partial
load shipping.)
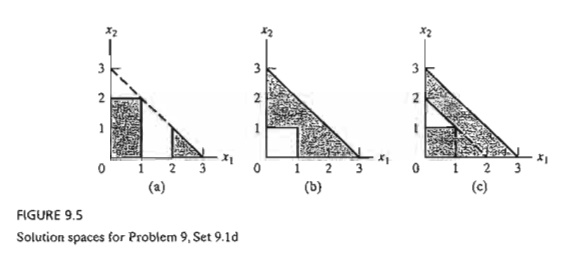
8. Show how the nonconvex shaded solution spaces in Figure 9.5 can be
represented by a set of simultaneous constraints. Find the optimum solution
that maximizes z = 2x\ + 3X2 subject to the solution space
given in (a).
9. Suppose that it is required that any k out of the following m constraints must be active:
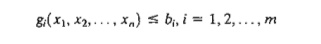
Show how this condition may be represented.
10. In the following constraint, the right-hand side may assume one of
values, bI, b2 , .. , and bm
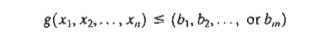
Related Topics