B&B Solution Algorithm - Traveling Salesperson Problem (TSP)

B&B Solution Algorithm

The idea of the B&B algorithm is to start with the optimum solution of the associated assignment problem. If the solution is a tour, the process ends. Otherwise, restrictions are imposed to remove the subtours. This can be achieved by creating as many branch-es as the number of x_ij variables associated with one of the subtours. Each branch will correspond to setting one of the variables of the subtour equal to zero (recall that all the variables associated with a subtour equal 1). The solution of the resulting assign-ment problem mayor may not produce a tour. If it does, we use its objective value as an upper bound on the true minimum tour length. If it does not, further branching is necessary, again creating as many branches as the number of variables in one of the subtours. The process continues until all unexplored subproblems have been fathomed, either by producing a better (smaller) upper bound or because there is evidence that the subproblem cannot produce a better solution. The optimum tour is the one associ-ated with the best upper bound.

The following example provides the details of the TSP B&B algorithm.

Example 9.3-4

Consider the following 5-city TSP problem:

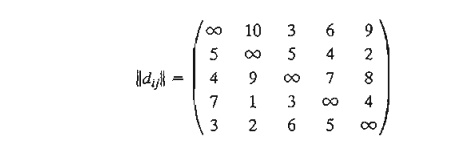
We start by solving the associated assignment, which yields the following solution:

z = 15, (x₁₃ =  x₃₁  = 1), (x₂₅  = x₅₄  = x₄₂  =  1), all others = 0

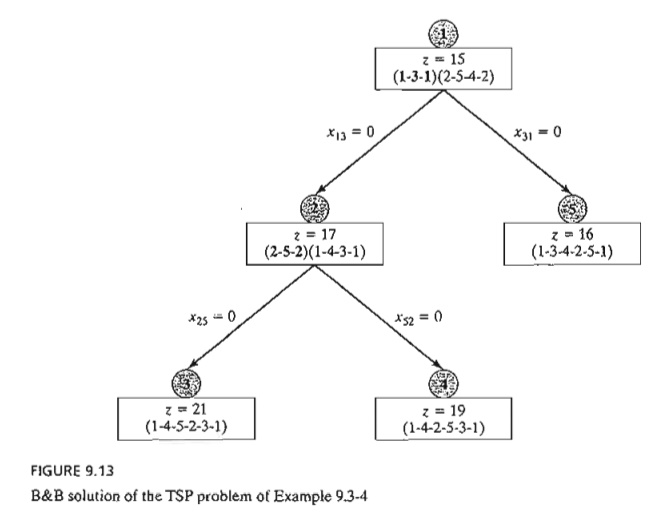
This solution yields two subtours: (1-3-1) and (2-5-4-2), as shown at node 1 in Figure 9.13. The associated total distance is z = 15, which provides a lower bound on the optimal length of the 5-city tour.

A straightforward way to determine an upper bound is to select any tour and use its length as an upper bound estimate. For example, the tour 1-2-3-4-5-1 (selected totally arbitrarily) has a total length of 10 + 5 + 7 + 4 + 3 = 29. Alternatively, a better upper bound can be found by applying the heuristic of Section 9.3.1. For the moment, we will use the upper bound of length 29 to apply the B&B algorithm. Later, we use the "improved" upper bound obtained by the heuristic to demonstrate its impact on the search tree.

The computed lower and upper bounds indicate that the optimum tour length lies in range (15, 29). A solution that yields a tour length larger than (or equal to) 29 is discarded as nonpromising.

To eliminate the subtours at node 1, we need to "disrupt" its loop by forcing its member variables, x_ij, to be zero. Subtour 1-3-1 is disrupted if we impose the restriction x_l3 = 0 or x₃₁ = 0 (i.e., one at a time) on the assignment problem at node 1. Similarly, subtour 2-5-4-2 is eliminated by imposing one of the restrictions x₂₅ = 0, x₅₄ = 0, or x₄₂ = 0. In terms of the B&B tree, each of these restrictions gives rise to a branch and hence a new subproblem. It is important to notice that branching both subtours at node 1 is not necessary. Instead, only one subtour needs to be disrupted at anyone node. The idea is that a breakup of one subtour automatically alters the member variables of the other subtour and hence produces conditions that are favorable to creating a tour. Under this argument, it is more efficient to select the subtour with the smallest number of cities because it creates the smallest number of branches.

Targeting subtour (1-3-1), two branches x₁₃ = 0 and x₃₁ = 0 are created at node 1. The associated assignment problems are constructed by removing the row and column associated with the zero variable, which makes the assignment problem smaller. Another way to achieve the same result is to leave the size of the assignment problem unchanged and simply assign an infinite distance to the branching variable. For example, the assignment problem associated with x_l3 = 0 requires substituting d₁₃ = ¥ in the assignment model at node 1. Similarly, for x₃₁ = 0, we substitute d₃₁ = ¥.

In Figure 9.13, we arbitrarily start by solving the subproblem associated with x₁₃ = 0 by setting d_l3 = ¥, Node 2 gives the solution z = 17 but continues to produce the subtours (2-5-2) and (1-4-3-1). Repeating the procedure we applied at node 1 gives rise to two branches: x₂₅ = 0 and x₅₂ = 0.

We now have three unexplored subproblems, one from node 1 and two from node 2, and we are free to investigate any of them at this point. Arbitrarily exploring the subproblem associated with x₂₅ = 0 from node 2, we set d₁₃ = ¥ and d₂₅ = ¥ in the original assignment problem, which yields the solution z = 21 and the tour solution 1-4-5-2-3-1 at node 3. The tour solution at node 3 lowers the upper bound from z == 29 to z == 21. This means that any unexplored subproblem that can be shown to yield a tour length larger than 21 is discarded as nonpromising.

We now have two unexplored subproblems. Selecting the subproblem 4 for exploration, we set d_l3 = ¥ and d₅₂ = ¥ in the original assignment, which yields the tour solution 1-4-2-5-3-1 with z = 19. The new solution provides a better tour than the one associated with the current upper bound of 21. Thus, the new upper bound is updated to z = 19 and its associated tour, 1-4-2-5-3-1, is the best available so far.

Only subproblem 5 remains unexplored. Substituting d₃₁ = ¥ in the original assignment problem at node 1, we get the tour solution 1-3-4-2-5-1 with z = 16, at node 5. Once again, this is a better solution than the one associated with node 4 and thus requires updating the upper bound to z = 16.

There are no remaining unfathomed nodes, which completes the search tree. The optimal tour is the one associated with the current upper bound: 1-3-4-2-5-1 with length 16 miles.

Remarks. The solution of the example reveals two points:

1. Although the search sequence 1 -> 2 -> 3 -> 4 -> 5 was selected deliberately to demonstrate the mechanics of the B&B algorithm and the updating of its upper bound, we generally have no way of predicting which sequence should be adopted to improve the efficiency of the search. Some rules of thumb can be of help. For example, at a given node we can start with the branch associated with the largest d_ij among all the created branches. By canceling the tour leg with the largest d_ij, the hope is that a "good" tour with a smaller total length will be found. In the present example, this rule calls for exploring branch x₃₁ == 0 to node 5 be-fore branch x₁₃ to node 2 because (d₃₁ == 4) > (d₁₃ == 3), and this would have produced the upper bound z == 16, which automatically fathoms node 2 and, hence, eliminates the need to create nodes 3 and 4. Another rule calls for sequencing the exploration of the nodes in a horizontal tier (rather than vertically). The idea is that nodes closer to the starting node are more likely to produce a tighter upper bound because the number of additional constraints (of the type x_ij = 0) is smaller. This rule would have also discovered the solution at node 5 sooner.

2. The B&B should be applied in conjunction with the heuristic in Section 9.3.1. The heuristic provides a "good" upper bound which can be used to fathom nodes in the search tree. In the present example, the heuristic yields the tour 1-3-4-2-5-1 with a length of 16 distance units.

AMPl Moment

Interactive AMPL commands are ideal for the implementation of the TSP B&B algorithm using the general assignment model (file ampIAssignment.txt). The following table summarizes the AMPL commands needed to create the B&B tree in Figure 9.13 (Example 9.3-4):

PROBLEM SET 9.3C

1. Solve Example 9.3-3 using subtour 2-5-4-2 to start the branching process at node 1, using the following sequences for exploring the nodes.

a)      Explore all the subproblems horizontally from left to right in each tier before preceeding to the next tier.

b)      Follow each path vertically from node 1 until it ends with a fathomed node.

*2. Solve Problem 1, Set 9.3a using B&B.

3. Solve Problem 2, Set 9.3a using B&B.

4. Solve Problem 3, Set 9.3a using B&B.