Cutting Plane Algorithm - Traveling Salesperson Problem (TSP)

Cutting-Plane Algorithm

The idea of the cutting plane algorithm is to add a set of constraints to the assignment problem that prevent the formation of a subtour. The additional constraints are defined as follows. In an n-city situation, associate a continuous variable u_j (≥ 0) with cities 2, 3, ... , and n. Next, define the required set of additional constraints as

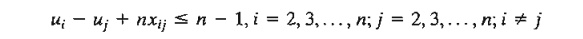
These constraints, when added to the assignment model, will automatically remove all subtour solutions.

Example 9.3-5

Consider the following distance matrix of a 4-city TSP problem.

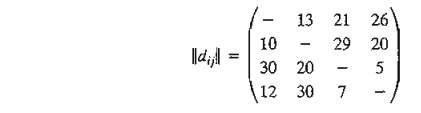
The associated LP consists of the assignment model constraints plus the additional constraints in the table below. All x_ij = (0, 1) and all u_j ≥ 0.

This corresponds to the tour solution 1-2-3-4-1. The solution satisfies all the additional constraints in u_j (verify!).

To demonstrate that subtour solutions do not satisfy the additional constraints, consider (1-2-1,3-4-3), which corresponds to x₁₂ = x₂₁ = 1, x₃₄ = x₄₃ = 1. Now, consider constraint 6 in the tableau above:

Substituting x₄₃ = 1, u₃ = 2, u₄ = 3 yields 5 ≤ 3, which is impossible, thus disallowing x₄₃ = 1 and subtour 3-4-3.

The disadvantage of the cutting-plane model is that the number of variables grows exponentially with the number of cities, making it difficult to obtain a numeric solution for practical situations. For this reason, the B&B algorithm (coupled with the heuristic) may be a more feasible alternative for solving the problem.

AMPL Moment

Figure 9.14 provides the AMPL model of the cutting-plane algorithm (file amplEx9.3-5.txt). The data of the 4-cityTSP of Example 9.3-5 are used to drive the model. The for-mulation is straightforward: The fIrst two sets of constraints define the assignment model associated with the problem, and the third set represents the cuts needed to re-move subtour solutions. Notice that the assignment-model variables must be binary and that option solver cplex; must precede solve; to ensure that the obtained so-lution is integer.

The for and if - then statements at the bottom of the model are used to present the out-put in the following readable format:

PROBLEM SET 9.3 D

1. An automatic guided vehicle (AGV) is used to deliver mail to 5 departments located on a factory floor. The trip starts at the mail sorting room and makes the delivery round to the different departments before returning to the mailroom. Using the mailroom as the origin (0,0), the (x, y) locations of the delivery spots are (10,30), (10, 50), (30, 10), (40,40), and (50,60) for departments 1 through 5, respectively. All distances are in meters. The AGV can move along horizontal and vertical aisles only. The objective is to minimize the length of the round trip.

Formulate the problem as a TSP, including the cuts.

2. Write down the cuts associated with the following TSP:

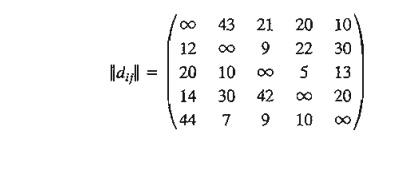
3. AMPL experiment. Use AMPL to solve the following TSP problem by the cutting plane algorithm.

a)      Problem 2, Set 9.3a.

b)     Problem 3, Set 9.3a.