Chapter: Operations Research: An Introduction : Integer Linear Programming
Capital Budgeting- Integer Linear Programming Illustrative Applications
ILLUSTRATIVE APPLICATIONS
This section presents a number of ILP applications. The applications
generally fall into two categories: direct
and transformed. In the direct category, the variables are
natural-ly integer and may assume binary (0 or 1) or general discrete values.
For example, the problem may involve determining whether or not a project is
selected for execution (binary) or finding the optimal number of machines
needed to perform a task (general discrete value). In the transfonned category, the original problem, which may not involve
any integer variables, is analytically intractable. Auxiliary integer variables
(usu-ally binary) are used to make it tractable. For example, in sequencing two
jobs, A and B, on a single machine, job A
may precede job B or job B may precede job A. The "or" nature
of the constraints is what makes the problem analytically intractable, because
all mathematical programming algorithms deal with "and" constraints
only. The situa-tion is remedied by using auxiliary binary variables to
transform the "or" constraints into equivalent "and" constraints.
For convenience, a pure integer problem is defined to have all integer variables. Otherwise, a
problem is a mixed integer program if it deals with both continuous and integer
variables.
1. Capital Budgeting
This section deals with decisions regarding whether or not investments
should be made in individual projects. The decision is made under
limited-budget considerations as well as priorities in the execution of the
projects.
Example 9.1-1 (Project
Selection)
Five
projects are being evaluated over a 3-year planning horizon. The following
table gives the expected returns for each project and the associated yearly
expenditures.
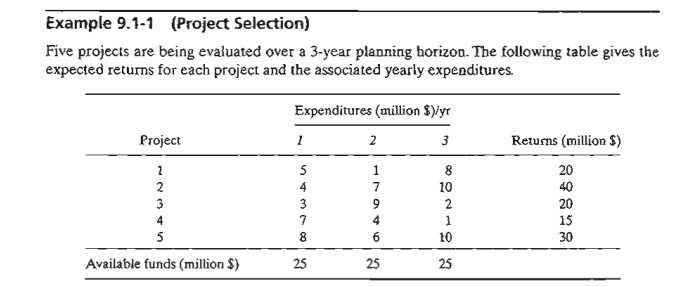
Which
projects should be selected over the 3-year horizon?
The
problem reduces to a "yes-no" decision for each project. Define the
binary variable xj as

The
optimum integer solution (obtained by AMPL, Solver, or TORA) is x1 =x2
= x3
= x4
= 1, x5 = 0, with z = 95
(million $). The solution shows that all but project 5 must be selected.
Remarks. It is interesting to compare the
continuous LP solution with the ILP solution. The LP
optimum, obtained by replacing xj = (0,1) with 0 ≤ xj ≤ 1 for all j, yields x1
= .5789, x2
= x3
= x4 = 1, x5 = .7368, and z = 108.68 (million $). The
solution is meaningless because two of the variables assume
fractional values. We may round the
solution to the closest integer values, which yields x1 = x5 = 1. However, the resulting
solution is infeasible because the constraints are violated. More important,
the concept of rounding is
meaningless here because xi
rep-resents a "yes-no" decision.
PROBLEM SET 9.1A
1. Modify and solve the capital budgeting model of Example 9.1-1 to account for the fol-lowing
additional restrictions:
a) Project 5 must be
selected if either project 1 or
project 3 is
selected.
b) Projects 2 and 3 are mutually exclusive.
2. Five
items are to be loaded in a vessel. The weight wi, volume vi, and
value ri for item i are
tabulated below.
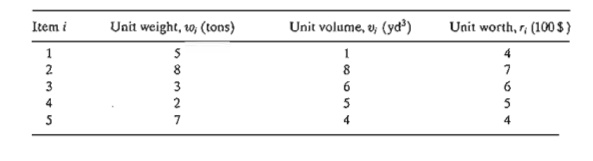
The
maximum allowable cargo weight and volume are 112 tons and 109 yd3 ,
respectively. Formulate the ILP model, and find the most valuable cargo.
*3. Suppose that you have 7 full wine bottles, 7 half-full, and 7 empty.
You would like to divide the 21 bottles among three individuals so that each
will receive exactly 7. Addition-ally, each individual must receive the same
quantity of wine. Express the problem as ILP constraints, and find a solution. (Hint: Use a dummy objective function in
which all the objective coefficients are zeros.)
4. An eccentric sheikh left a will to distribute a herd of camels among
his three children: Tarek receives at least one-half of the herd, Sharif gets
at least one third, and Maisa gets at least one-ninth. The remainder goes to
charity. The will does not specify the size of the herd except to say that it
is an odd number of camels and that the named charity receives exactly one
camel. Use ILP to determine how many camels the sheikh left in the estate and
how many each child got.
5. A farm couple are sending their three children to the market to sell
90 apples with the objective of educating them about money and numbers. Karen,
the oldest, carries 50 apples; Bill, the middle one, carries 30; and John, the
youngest, carries only 10. The parents have stipulated five rules: (a) The
selling price is either $1 for 7 apples or $3 for 1 apple, or a combination of
the two prices. (b) Each child may exercise one or both options of the selling
price. (c) Each of the three children must return with exactly the same amount
of money. (d) Each child's income must be in whole dollars (no cents allowed).
(e) The amount received by each child must be the largest possible under the
stipulated condi-tions. Given that the three kids are able to sell all they
have, use ILP to show how they can satisfy the parents' conditions.
*6. Once upon a time, there was a captain of a merchant ship who wanted
to reward three crew members for their valiant effort in saving the ship's
cargo during an unexpected storm in the high seas. The captain put aside a
certain sum of money in the purser's office and instructed the first officer to
distribute it equally among the three mariners after the ship had reached
shore. One night, one of the sailors, unbeknown to the others, went to the
purser's office and decided to claim (an equitable) one-third of the money in
advance. After he had divided the money into three equal shares, an extra coin
remained, which the mariner decided to keep (in addition to one-third of the
money). The next night, the second mariner got the same idea and, repeating the
same three-way division with what was left, ended up keeping an extra coin as
well. The third night, the third mariner also took a third of what was left,
plus an extra coin that could not be divided. When the ship reached shore, the
first officer divided what was left of the money equally among the three
mariners, again to be left with an extra coin. To simplify things, the first
officer put the extra coin aside and gave the three mariners their allotted
equal shares. How much money was in the safe to start with? Formulate the
problem as an ILP, and find the solution. (Hint:
The problem has a countably infinite number of integer solutions. For
convenience, assume that we are interested in determining the smallest sum of
money that satisfies the problem conditions. Then, boosting the resulting sum
by 1, add it as a lower bound and obtain the next smallest sum. Continuing in
this manner, a general solution pattern will evolve.)
7. (Weber, 1990) You have the following three-letter words: AFT, FAR,
TVA, ADV, JOE, FIN, OSF, and KEN. Suppose that we assign numeric values to the
alphabet starting with A = 1 and
ending with Z = 26. Each word is scored by adding numeric codes of its three letters. For example, AFT has a
score of 1 + 6 + 20 = 27. You
are to select five of the given eight words that yield the maximum total score.
Simultaneously, the selected five words must satisfy the following conditions:
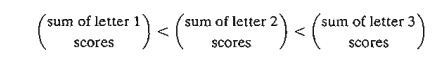
Formulate the problem as an ILP, and find the optimum solution.
8. Solve Problem 7 given that, in addition to the total sum being the
largest, the sum of col-umn 1 and the sum of column 2 will be the largest as
well. Find the optimum solution.
9. (Weber, 1990) Consider the following two groups of words:

All the words in groups 1 and 2 can be formed from the nine letters A,
E, F, H, 0, P, R, S, and T. Develop a model to assign a unique numeric value from 1
through 9 to these let-ters such that the difference between the total scores
of the two groups will be as small as possible. [Note: The
score for a word is the sum of the numeric values assigned to its individual
letters.]
*10. The Record-a-Song Company has contracted with a rising star to
record eight songs. The durations of the different songs are 8,3,5,5,9,6,7, and
12 minutes, respectively. Record-a-Song uses a two-sided cassette tape for the
recording. Each side has a capacity of 30 minutes. The company would like to
distribute the songs between the two sides such that the length of the songs on
each side is about the same. Formulate the problem as an ILP, and find the
optimum solution.
11. In Problem 10, suppose that the nature of the melodies dictates that
songs 3 and 4 cannot be recorded on the same side. Formulate the problem as an
ILP. Would it be possible to use a 25-minute tape (each side) to record the
eight songs? If not, use ILP to determine the minimum tape capacity needed to make the
recording.
*12. (Graves and Associates, 1993) Ulem University uses a mathematical
model that optimizes student preferences taking into account the limitation of
classroom and faculty re-sources. To demonstrate the application of the model,
consider the simplified case of 10 students who are required to select two
courses out of six offered electives. The table below gives scores that
represent each student's preference for individual courses, with a score of 100
being the highest. For simplicity, it is assumed that the preference score for
a two-course selection is the sum of the individual score. Course capacity is
the maximum number of students allowed to take the class.
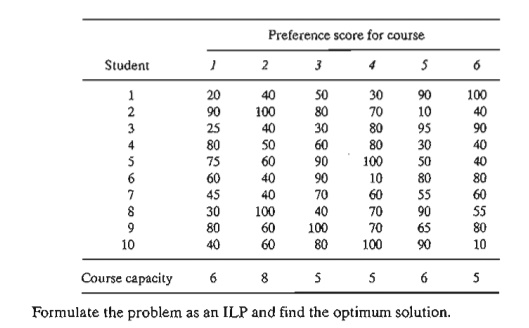
Related Topics