Division of Fractions

Division of Fractions

Think about the situation 1

A camp was organized in a school in which 12 students participated. The camp leader wanted to divide them into groups of 2 students. How many groups were there?

There were 6 groups which was got by the division of 12 by 2.

That is 12 ÷ 2 = 6 which means there are six 2’s in 12.

If the camp leader distributes 6 litres of water in ½ litre water bottles to the students, then how many students will get water bottles? This means finding how many 1/2 litres are there in 6 litres. For this we need to calculate 6 ÷ 1/2 .

 Solution

 Let us describe the situation

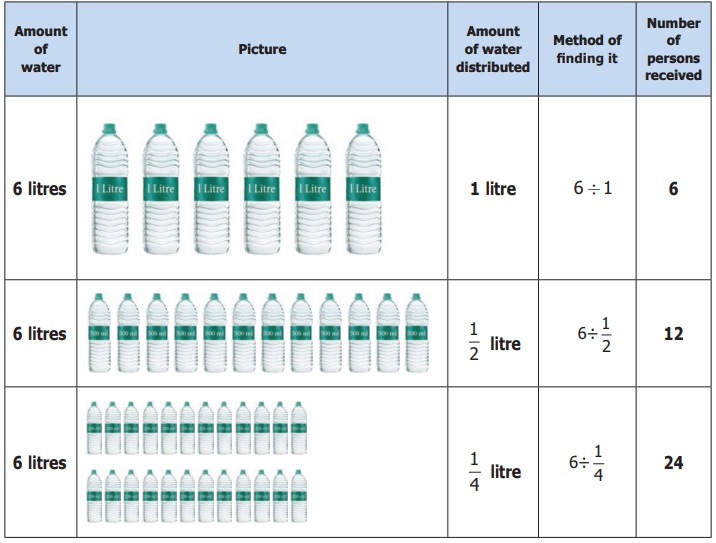
This means that if you share 6 litres of water into 1 litre bottles, 6 persons can get water. If you share in 1/2 litre water bottles, 12 persons can get water. If you share it in 1/4 litre water bottles, 24 persons can get water. That is

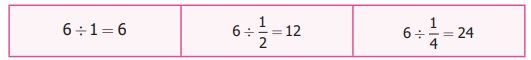
We can illustrate this in the following diagram. We divide each circle into halves such that each part is 1/2 of the whole. The number of such halves would be 6 ÷ 1/2. In the figure how many halves do you see? There are 12 halves. So 6 ÷ ½ = 6 × 2 = 12 .

As one circle has 2 halves, 6 circles will have 12 halves = 6 × 2. Therefore, 6 ÷ 1/2 = 6 × 2 = 12

Here, we can observe that, dividing a whole number 6 by a fraction 1/2 is the same as multiplying a whole number 6 by 2, where 2 is the reciprocal of 1/2 . Generally, dividing a number by a fraction is the same as multiplying that number by the reciprocal of the fraction.

Let us discuss the same situation in another way. Let us take a bar of length 12 cm How many 2 cm bars are there in a 12 cm bar?

Now find how many 1/2 cm bars are there in a 12 cm bar?

Let us observe and complete the following:

i) 3/7 × 7/3 = 21/21 = 1

ii) 1/9 × 9 = 9/9 = 1

iii) 8 × 1/8 = 8/8 = ?

iv) 13/4 × ? = 1

v) 4/3 × ? = 1

From the above, we can see that the Product of a fraction and its reciprocal is always 1.

Example 19

Kandan shares 1/ 2 piece of a cake between 2 persons. What will be the share 2 of each?

Solution

 To know the share, we need to find 1/2 ÷ 2

1/2 ÷ 2 = 1/2 × 1/2 (reciprocal of 2 is 1/2)

= 1/2 ÷ 2 = 1/2 × 1/2 (reciprocal of 2 is 1/2)

= 1/2 × 1/2 = [1 × 1] / [2 × 2] = 1 / 4

Try these

i) How many 6s are there in 18?

Three 6 s are in 18.

ii) How many ¼ s are there in 5?

Twenty 1/4 s are there in 5.

iii) 1/3 ÷ 5=?

1/3 ÷ 5 = 1/3 × 1/5 = 1/15

Example 20

Divide 4 1/2 by 3 1/2

Solution

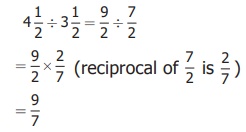
Example 21

An oil tin contains 7 1/2 litres of oil which is poured in 2 1/2 litres bottles. How many bottles are required to fill 7 1/2  litres oil?

Solution

The number of bottles required = 15/2 ÷ 5/2 = 15/2 × 2/5 (reciprocal of 5/2 is 2/5)

= 3 bottles

Example 22

 A rod of length 6m is cut into small rods of length 1 ½  m each. How many  small rods can be cut?

Solution

The number of small rods = 6 ÷ 1 (1/2)

                                          = 6 ÷ 3/2

  = 6 × 2/3 (reciprocal of 3/2 is 2/3 )

 = 4 rods

Try these

i) Find the value of 5 ÷ 2(1/2).

= 5 ÷ 2 1/2  = 5 ÷ 5/2.

= 5 × 2/5 = 2

ii) Simplify: 1(1/2) ÷ 1/2

3/2 ÷ 1/2

3/2 × 2/1 = 3

iii) Divide 8 ½ by 4 ¼.

8 1/2 ÷ 4 1/4

17/2 ÷ 17/4

17/2 ÷ 4/17 = 2

ICT CORNER

Fractions

Expected Outcome

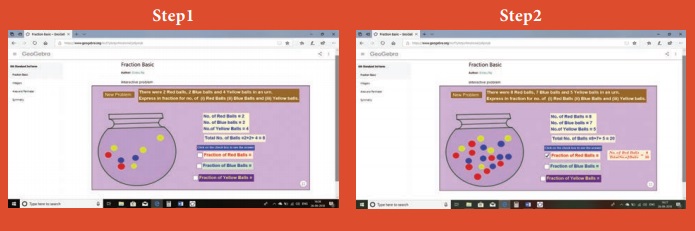
Step 1

Open the Browser by typing the URL Link given below (or) Scan the QR Code. GeoGebra work sheet named “Fraction Basic” will open. Click on New Problem and solve the problem.

Step 2

Click the check boxes on right hand side bottom to check respective answers

Browse in the link:

Fraction Basic: https://ggbm.at/jafpsnjb or Scan the QR Code.

This puzzle involves fraction in Tamil song and its explanation

கட்டியால் எட்டு கட்டி

கால்அரை முக்கால் மாற்று

வியாபாரி சென்று விட்டார்

சிறுபிள்ளை மூன்று பேர்கள்

கட்டியும் புக் கொணாது

கணக்கிலும் பிச கொணாது

கட்டியாய் பகர வல்லார்

கணககினில் வல்லா ராவார்

Explanation

A jaggery merchant had 8 jaggery balls with different weights such as 1/4  kg 1 /2   kg and 3/4 kg. He called his 3 children and asked them to share those jaggery balls equally. How did the children share it equally among themselves? (Hint: The number of jaggery balls with the given weights are 5, 2 and 1 respectively.).