Addition and Subtraction of Mixed Fractions

Addition and Subtraction of Mixed Fractions

Think about the situation

In a joint family of Saravanan, during pongal festival celebration, his grandfather, his father and himself wanted to wear the same colour shirt. The cloth needed for stitching 3 shirts are 2 3/4 m, 2 1/2 m and 1 1/4 m respectively. How many metres of cloth has to be purchased in total?

So the total length of the cloth bought by his father is 2 3/4 + 2 1/2 +1 1/4 . This is solved in the following example.

Example 12

Saravanan’s father bought 2 3/4 m , 2 1/2 m and 1 1/4 m  of cloth. Find the total  length of the cloth bought by him?

Solution

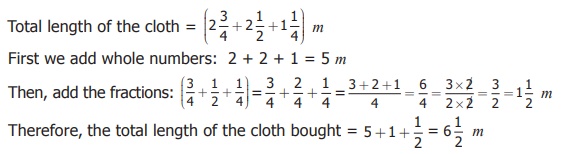
Example 13

 Add: 3 2/4 + 7 2/5

Solution 3 2/4 + 7 2/5 = 3 + 2/4 + 7 + 2/5

= 3 + 7 + (2/4 + 2/5)

= 10 + (10/20 + 8/20)

= 10 + 18/20 = 10 + 9/10 =10 9/10

Think about the situation

One day Anitha’s mother bought 5 1/2 litres of milk. She has used only 3 1/4 litres of milk to prepare payasam. How much milk is left? That is 5 1/2 – 3 1/4.

Example 14

In the above situation, find the quantity of milk left over. So, subtract 3 1/4 from 5 1/2

Solution

The quantity of milk left over = 5 1/2 − 3 1/4

Here, note that 5 > 3 and 1/2 > 1/4

The whole numbers 5 and 3 and the fractional numbers 1/2 and 1/4 can be subtracted separately.

So 5 ½ − 3 ¼ = (5 – 3) + (1/2 – 1/4)

= 2 + (2/4 -1/4) (Since the equivalent fraction of 1/2 is 2/4)

= 2 + 1/4 = 2 1/4 liters

Note

This method is applicable only when both integral and fractional parts of minuend is greater than that of the subtrahend.

Example 15

Simplify: 9 1/4 − 3 5/6

Solution

Here 9 > 3 and 1/4 < 5/6, So we proceed as follows:

We convert the mixed fraction into improper fraction and then subtract.

9 1/4 = [(9 × 4) + 1] / 4 = 37 / 4

And 3 5/6 = [(3 × 6) + 5] / 6 = 23/6

Common multiple of 4 and 6 is 12.

Now, 37/4 – 23/6 = [37 × 3] /12 – [23 × 2] / 12

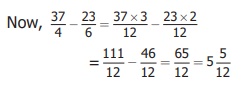
= 111/12 – 46/12 = 65/12 = 5 5/12

Try these

i) Find the sum of 5 4/9 and 3 1/6

5 4/9 + 3 1/6

49/9 + 19/6

[98 + 57] / 18 = 155/18

= 8 11/18

ii) Subtract 7 1/6 from 12 3/8.

12 3/8 – 7 1/6

99/8 – 43/6

[297 – 172] / 24 = 125/24

= 5 5/24

iii) Subtract the sum of 6 1/6 and 3 1/5 from the sum of 9 2/3 and 2 1/2.

= (9 2/3 + 2 1/2) – (6 1/6 + 3 1/5 )

= ( 29/3 + 5/2) – ( 37/6 + 16/5)

= ( 58 + 15/6) – ( 185 + 96/30)

= 73/6 – 281/30

= 365 – 281/30 = 84/30 = 2  24/30 = 2 4/5