Comparison of Unlike Fractions

Comparison of Unlike Fractions

Think about the situation 1

Murugan has scored 7/10 in Science and 9/10 in Mathematics test. In which subject he has performed better? It is quite easy to say his performance is better in Mathematics.

But can you find, the better performance of Murugan between the two test scores such as 9/10 and 13/20 in Mathematics. We need to convert both the marks as like fractions.

 The equivalent fraction of 9/10 is 18/20.  Now we can compare the first test score with that of the second test score because both the scores are out of 20 marks. Here 18 > 13. So, 18/20 > 13/20 . Thus, Murugan has performed better in the first test.

Think about the situation 2

In a Hockey tournament, Team A played 6 matches and won 5 matches out of it. Team B played 5 matches and won 4 matches out of it. If both the teams performed consistently in this way, find out which team will win the tournament?

From these we need to see which is greater 5/6 or 4/5? How can we find this? The total number of matches played by each team differs. By finding the equivalent fractions of 5/6 and 4/5, we can equalize the number of matches played by team A and team B.

5/6 = 10/12 = 15/18 = 20/24 = 25/30

4/5 = 8/10= 12/15 = 20/25 = 24/30

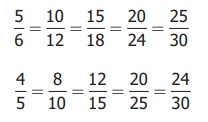
Note that the common denominator of equivalent fraction is 30, which is 5 × 6.

It is the common multiple of both 5 and 6.

 Here 25/30 > 24/30 . So Team A will win the game.

Note

To compare two or more unlike fractions, we have to convert them into 'like fractions'. These 'like fractions' are the equivalent fractions of the given fractions. The denominator of the 'like fractions' is the Least Common Multiple (LCM) of the denominators of the given unlike fractions.

Example 2

Madhu ate 2/5 of the chocolate bar and Nandhini ate 1/3 of the chocolate bar. Who has eaten more?

Solution

The portion of the chocolate eaten by Madhu = 2/5

The portion of the chocolate eaten by Nandhini = 1/3

Here the portions of the chocolates eaten by both differ.

To make it same, their equivalent fractions are to be found.

Finding the equivalent fractions of  2/5 and 1/3 having common denominators are the same as finding the least common multiple of the denominators of the given fractions.

Hence 2/5 = [2 × 3] / [5 × 3] = 6/15 and 1/3 = [1 × 5] / [3 × 5] = 5/15 So, 6/15 > 5 /15

 Therefore, we can conclude that Madhu has eaten more chocolates.

Note

The process of finding the like fractions of the given unlike fractions can be made easier by finding the common multiples of the denominators of the unlike fractions.

Example 3

 Vinotha, Mugilarasi, Senthamizh were participating in the water filling competition. Each one was given a bottle of equal volume to fill water in it within 30 seconds. If Vinotha filled 1/2 portion of her bottle, Senthamizh filled 3/4 portion of her bottle and Mugilarasi filled 1/4 portion of her bottle, then who would get the first, second and third prize?

Solution

The equivalent fractions need to be written until the denominator becomes 4 which is the LCM of 2 and 4.

Equivalent fraction of 1/2 is 2/4

Here 1/4  < 2/4   < 3/4 . Therefore, Senthamizh would get the first prize, Vinotha would get the second prize and Mugilarasi would get the third prize.

Example 4

 Arrange 2/3 , 1/6 , 4/9  in ascending order.

Solution  

Equivalent fractions of 2/3 are 4/6, 4/6, 6/9, 8/12, 10/15, 12/18, ….

Equivalent fractions of 1/6 are 2/12, 3/18,..

Equivalent fraction of 4/9 is 8/18,…

Therefore 3/18 < 8/18 < 12/18   

The ascending order of given fractions is 1/6, 4/9 , 2/3.

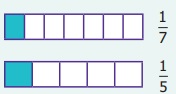
Comparison of Unit Fractions: Unit fractions are fractions having 1 as its numerator. For example compare 1/7 and 1/5 . One can conclude that 1/5 > 1/7 by observing the diagram. So, in unit fraction the larger the denominator the smaller will be the fraction. Hence, we conclude that if the numerators are the same in two fractions, the fraction with the smaller denominator is greater of the two.

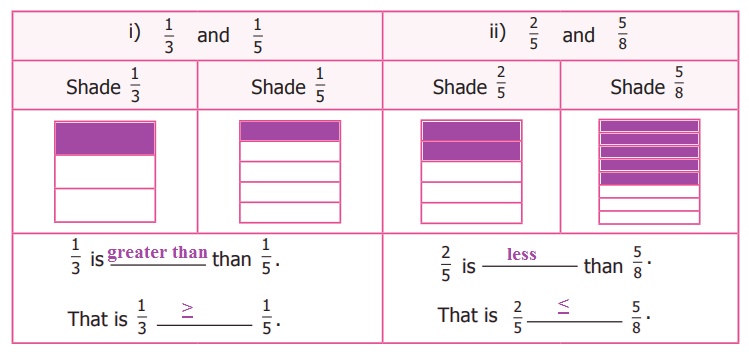
Try these

1. Shade the rectangle for the given pair of fractions and say which is greater among them.

2. Which is greater 3/8 or 3/5?

 3/5 is greater

3. Arrange the fractions in ascending order: 3/5, 9/10 , 11/15

 3/5, 11/15, 9/10

4. Arrange the fractions in descending order: 9/20, 3/4 , 7/12

3/4, 7/12, 9/20