Detection Limits

Detection Limits

A method’s detection limit is the smallest amount or concentration of analyte that can be detected with statistical confidence. The International Union of Pure and Applied Chemistry (IUPAC) defines the detection limit as the smallest concen- tration or absolute amount of analyte that has a signal significantly larger than the signal arising from a reagent blank. Mathematically, the analyte’s signal at the detec- tion limit, (S_A)_DL, is

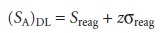               4.25

where S_reag is the signal for a reagent blank, σ_reag is the known standard devia- tion for the reagent blank’s signal, and z is a factor accounting for the desired confidence level. The concentration, (C_A)_DL, or absolute amount of analyte, (n_A)_DL, at the detection limit can be determined from the signal at the detection limit.

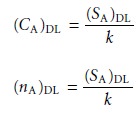
The value for z depends on the desired significance level for reporting the detection limit. Typically, z is set to 3, which, from Appendix 1A, corresponds to a signifi- cance level of α = 0.00135. Consequently, only 0.135% of measurements made on the blank will yield signals that fall outside this range (Figure 4.12a). When σ_reag is unknown, the term zσ_reag may be replaced with ts_reag, where t is the appropriate value from a t-table for a one-tailed analysis.

In analyzing a sample to determine whether an analyte is present, the signal for the sample is compared with the signal for the blank. The null hypothesis is that the sample does not contain any analyte, in which case (S_A)_DL and S_reag are identical. The alternative hypothesis is that the analyte is present, and (S_A)_DL is greater than S_reag. If (S_A)_DL exceeds S_reag by zσ(or ts), then the null hypothesis is rejected and there is evidence for the analyte’s presence in the sample. The proba- bility that the null hypothesis will be falsely rejected, a type 1 error, is the same as the significance level. Selecting z to be 3 minimizes the probability of a type 1 error to 0.135%.

Significance tests, however, also are subject to type 2 errors in which the null hypothesis is falsely retained. Consider, for example, the situation shown in Figure 4.12b, where S_A is exactly equal to (S_A)_DL. In this case the probability of a type 2 error is 50% since half of the signals arising from the sample’s population fall below the detection limit. Thus, there is only a 50:50 probability that an analyte at the IUPAC detection limit will be detected. As defined, the IUPAC definition for the detection limit only indicates the smallest signal for which we can say, at a significance level of α, that an analyte is present in the sample. Failing to detect the analyte, however, does not imply that it is not present.

An alternative expression for the detection limit, which minimizes both type 1 and type 2 errors, is the limit of identification, (S_A)_LOI, which is defined as

As shown in Figure 4.12c, the limit of identification is selected such that there is an equal probability of type 1 and type 2 errors. The American Chemical Society’s Committee on Environmental Analytical Chemistry recommends the limit of quantitation, (S_A)_LOQ, which is defined as

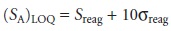
 Other approaches for defining the detection limit have also been developed.

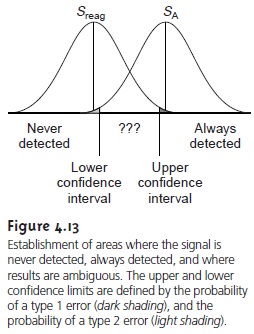
The detection limit is often represented, particularly when used in debates over public policy issues, as a distinct line separating analytes that can be detected from that cannot be detected.17 This use of a detection limit is incorrect. Defining the detection limit in terms of statistical confidence levels implies that there may be a gray area where the analyte is sometimes detected and sometimes not detected. This is shown in Figure 4.13 where the upper and lower confidence limits are de- fined by the acceptable probabilities for type 1 and type 2 errors. Analytes produc- ing signals greater than that defined by the upper confidence limit are always de- tected, and analytes giving signals smaller than the lower confidence limit are never detected. Signals falling between the upper and lower confidence limits, however, are ambiguous because they could belong to populations representing either the reagent blank or the analyte. Figure 4.12c represents the smallest value of S_A for which no such ambiguity exists.