Chapter: civil : Applied Hydraulic Engineering: Uniform Flow
Computations in Uniform Flow
Computations in Uniform Flow
We can use Manning's formula for
discharge to calculate steady uniform flow. Two calculations are usually
performed to solve uniform flow problems.
1. Discharge
from a given depth
2. Depth for
a given discharge
In steady
uniform flow the flow depth is know as normal depth.
As we have already mentioned, and
by definition, uniform flow can only occur in channels of constant
cross-section (prismatic channels) so natural channel can be excluded. However
we will need to use Manning's equation for gradually varied flow in natural channels
- so application to natural/irregular channels will often be required.
Uniform flow Problem 1 - Discharge from depth in a
trapezoidal channel
A concrete lined trapezoidal
channel with uniform flow has a normal depth is 2m. The base width is 5m and
the side slopes are equal at 1:2
Manning's n can be taken as 0.015 and the
bed slope S? = 0.001
What are: a) Discharge (Q) b) Mean velocity (V) c)
Reynolds number (Re) Calculate the section properties

This is very large - i.e. well
into the turbulent zone - the application of the Manning's equation was
therefore valid.
What solution would we have obtained if we had used the
Colebrook-White equation?
Probably very similar as we are
well into the rough-turbulent zone where both equations are truly applicable.
To experiment an
equivalent k s value can be calculated for the discharge
calculated from n = 0.015 and y = 2m [
ks = 2.225mm ] (Use
the Colebrook-White equation and the Darcy- Wiesbach equation of open channels
- both given earlier). Then a range
of depths can be chosen and the
discharges calculated for these n and
ks values. Comparing these discharge calculations will give some idea of
the relative differences - they will be very similar.
Uniform flow Problem 2 - Depth from Discharge in a
trapezoidal channel
Using the same channel as above,
if the discharge is know to be 30m3 /s in uniform flow, what is the
normal depth?
Again use equation
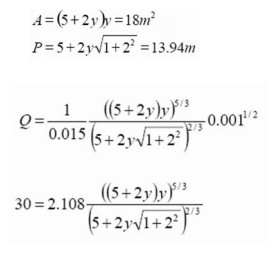
We need
to calculate y from this equation.
Even for this quite simple geometry the equation we need to
solve for normal depth is complex. One simple strategy to solve this is to
select some appropriate values of y and calculate the right hand side of
this equation and compare it to Q (=30) in the left. When it equals Q we have
the correct y .
Even though there will be several solutions to this equation,
this strategy generally works because we have a good idea of what the depth
should be (e.g. it will always be positive and often in the
range of 0.5-10 m). In this case from the previous
example we know that at Q = 45 m3 /s, y = 2m . So at Q = 30 m3
/s then y < 2.0m.

We might
also use the bisector method to solve this.
Uniform
flow Problem 3 - A compound channel
If the
channel in the above example were to be designed for flooding it may have a
section like this:

When
the flow goes over the top of the trapezoidal channel it moves to the
"flood plains" so the section allows for a lot more discharge to be
carried.
If
the flood channels are 10m wide and have side slopes of 1:3, and the
Manning n on these banks
is0.035, what are a) the discharge for a flood level of 4m b) the enery
coefficient a.
First split the section as shown
in to three regions (this is arbitrary - left to the engineers judgement). Then
apply Manning's formula for each section to give three discharge values and the
total discharge will be Q = Q1 + Q2 + Q 3 .
Calculate
the properties of each region:

This is a very
high value of a and a clear case of
where a velocity coefficient should be used.
Not that this method doe not give completely
accurate relationship between stage and discharge because some of the
assumptions are not accurate. E.g. the arbitrarily splitting in to regions of
fixed Manning n is probably not what is occurring in the actual channel.
However it will give an acceptable estimate as long as care is taken in
choosing these regions.
Related Topics