Applied Hydraulic Engineering: Uniform Flow - Fundamental equations

Fundamental equations

The equations which describe the flow of fluid are derived from three fundamental laws of physics:

1. Conservation of matter (or mass) 

2. Conservation of energy 

3. Conservation of momentum

Although first developed for solid bodies they are equally applicable to fluids. Brief descriptions of the concepts are given below.     

Conservation of matter 

This  says  that  matter  can  not  be created  nor  destroyed,  but  it  may  be  converted (e.g. by a chemical process.) In fluid mechanics we do not consider chemical activity so the law reduces to one of conservation of mass.    

Conservation of energy

This says that energy can not be created nor destroyed, but may be converted form one type to another (e.g. potential may be converted to kinetic energy). When engineers talk about energy "losses" they are referring to energy converted from mechanical (potential or kinetic) to some other form such as heat. A friction loss, for example, is a conversion of mechanical energy to heat. The basic equations can be obtained from the First Law of Thermodynamics but a simplified derivation will be given below.

Conservation of momentum

The law of conservation of momentum says that a moving body cannot gain or lose momentum unless acted upon by an external force. This is a statement of Newton's Second Law of Motion: Force = rate of change of momentum

In solid mechanics these laws may be applied to an object which is has a fixed shape and is clearly defined. In fluid mechanics the object is not clearly defined and as it may change shape constantly. To get over this we use the idea of control volumes. These are imaginary volumes of fluid within the body of the fluid. To derive the basic equation the above conservation laws are applied by considering the forces applied to the edges of a control volume within the fluid.

The Continuity Equation (conservation of mass)

For any control volume during the small time interval ?t the principle of conservation of mass implies that the mass of flow entering the control volume minus the mass of flow leaving the control volume equals the change of mass within the control volume.If the flow is steady and the fluid incompressible the mass entering is equal to the mass leaving, so there is no change of mass within the control volume.

So for the time interval ?t : Mass flow entering = mass flow leaving

Considering the control volume above which is a short length of open channel of arbitrary cross- Section then, if ? is the fluid density and Q is the volume flow rate then section then, if mass flow rate is ? Q and the continuity equation for steady incompressible flow can be written

pQ_entering = pQ_leaving

As, Q, the volume flow rate is the product of the area and the mean velocity then at the upstream face (face 1) where the mean velocity is u and the cross-sectional area is A1 then:

Q_entering = u₁A₁

Similarly at the downstream face, face 2, where mean velocity is u2 and the cross-sectional area is A2 then:

Q_leaving= u₂A₂

Therefore the continuity equation can be written as

u₁A₁ = u₂A₂

The Energy equation (conservation of energy):

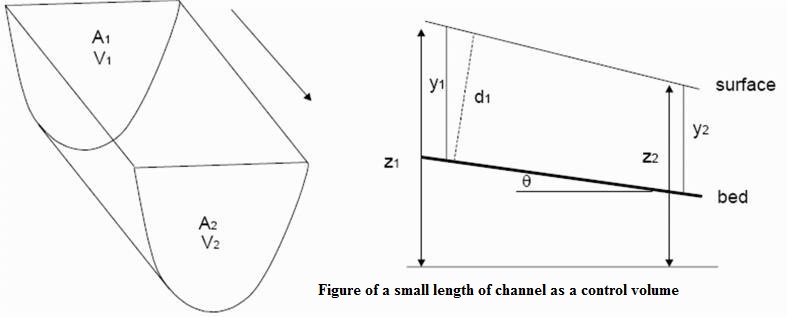
Consider the forms of energy available for the above control volume. If the fluid moves from the upstream face 1, to the downstream face 2 in time d t over the length L.

The work done in moving the fluid through face 1 during this time is

Where p1  is pressure at face 1

Work done = p₁A₁L

The mass entering through face 1 is

Mass entering = p₁A₁L

Therefore the kinetic energy of the system is:

KE = ½ mu² = ½ p₁A₁Lu₁²

If z1 is the height of the centroid of face 1, then the potential energy of the fluid entering the control volume is :

PE = mgz = p₁A₁Lgz₁

The total energy entering the control volume is the sum of the work done, the potential and the kinetic energy:

Total energy = p₁A₁L  +  ½ p₁A₁Lu₁²  + p₁A₁Lgz₁

We can write this in terms of energy per unit weight. As the weight of water entering the control volume is ?1 A1 L g then just divide by this to get the total energy per unit weight:

Total energy per unit weight = p1/p1g + u₁² + z₁

At the exit to the control volume, face 2, similar considerations deduce

Total energy per unit weight = p2/p2g + u₂² + z₂

If no energy is supplied to the control volume from between the inlet and the outlet then energy leaving = energy entering and if the in compressible

p1/p1g + u₁² + z₁  + p2/p2g + u₂² + z₂  = H = constant

This is the Bernoulli equation.

Note:

1.  In the derivation of the Bernoulli equation it was assumed that no energy is lost in the control volume - i.e. the fluid is frictionless. To apply to non frictionless situations some energy loss term must be included.

The dimensions of each term in equation 1.2 has the dimensions of length ( units of meters). For this reason each term is often regarded as a "head" and given the names

P/pg=pressure head

U²/2g = velocity head

Z=velocity or potential head

3. Although above we derived the Bernoulli equation between two sections it should strictly speaking be applied along a stream line as the velocity will differ from the top to the bottom of the section. However in engineering practise it is possible to apply the Bernoulli equation with out reference to the particular streamline

The momentum equation (momentum principle)

Again consider the control volume above during the time ?t

Momentum entering = p ?Q₁?tu₁

Momentum entering = p ?Q₂?tu₂

By the continuity principle :  = d Q1 = dQ 2 = dQ

And by Newton's second law Force = rate of change of momentum

It is more convenient to write the force on a control volume in each of the three, x, y and z direction e.g. in the x-direction

Integration over a volume gives the total force in the x-direction as

Fx = pQ(V_2x - V_1x)

As long as velocity V is uniform  over the whole cross-section.

This is the momentum equation for steady flow for a region of uniform velocity.

Energy and Momentum coefficients

In deriving the above momentum and energy (Bernoulli) equations it was noted that the velocity must be constant (equal to V) over the whole cross-section or constant along a stream-line.

Clearly this will not occur in practice. Fortunately both these equation may still be used even for situations of quite non-uniform velocity distribution over a section. This is possible by the introduction of coefficients of energy and momentum, a and ß respectively.

where V is the mean velocity.

And the Bernoulli equation can be rewritten in terms of this mean velocity:

P/pg + aV²/2g + z = constant

And the momentum equation becomes:

Fx = pQB(V_2x - V_1x)

The values of ? and ß must be derived from the velocity distributions across a cross-section. They will always be greater than 1, but only by a small amount consequently they can often be confidently omitted - but not always and their existence should always be remembered.

For turbulent flow in regular channel a does not usually go above 1.15 and ß will normally be below 1.05. We will see an example below where their inclusion is necessary to obtain accurate results.