Compiler Techniques for Exposing ILP

Compiler Techniques for Exposing ILP

1. Basic Pipeline Scheduling and Loop Unrolling

To avoid a pipeline stall, a dependent instruction must be separated from the source instruction by a distance in clock cycles equal to the pipeline latency of that source instruction.

A compiler’s ability to perform this scheduling depends both on the amount of ILP available in the program and on the latencies of the functional units in the pipeline. Throughout this chapter we will assume the FP unit latencies shown in Figure 1.7

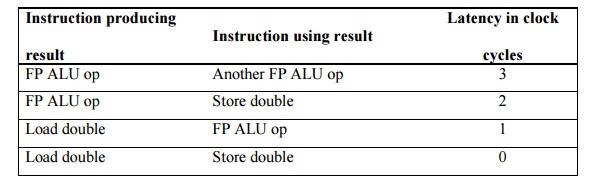
FIGURE 1.7 Latencies of FP operations used in this chapter.

The first column shows the originating instruction type. The second column is the type of the consuming instruction. The last column is the number of intervening clock cycles needed to avoid a stall.

We will rely on an example similar to the one we used in the last chapter, adding a scalar to a vector:

for (i=1000; i>0; i=i–1)

x[i] = x[i] + s;

This loop is parallel by noticing that the body of each iteration is independent. The first step is to translate the above segment to MIPS assembly language. In the following code segment, R1is initially the address of the element in the array with the highest address, and F2 contains the scalar value, s. Register R2 is precomputed, so that 8(R2) is the last element to operate on. The straightforward MIPS code, not scheduled for the pipeline, looks like this:

Loop:  L.D  F0,0(R1)     ;F0=array element

ADD.D       F4,F0,F2     ;add scalar in F2

S.D    F4,0(R1)     ;store result

DADDUI    R1,R1,#-8   ;decrement pointer

                   ;8 bytes (per DW)

BNE  R1,R2,Loop         ;branch R1!=zero

Let’s start by seeing how well this loop will run when it is scheduled on a simple pipeline for MIPS with the latencies

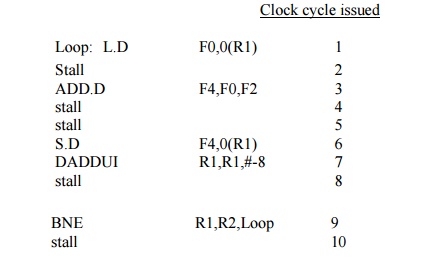
          Clock cycle issued

Loop:  L.D  F0,0(R1)     1

Stall            2

ADD.D       F4,F0,F2     3

stall             4

stall             5

S.D    F4,0(R1)     6

DADDUI    R1,R1,#-8   7

stall             8

BNE  R1,R2,Loop         9

stall             10

This code requires 10 clock cycles per iteration. We can schedule the loop to obtain only one stall:

Loop:  L.D  F0,0(R1)    

DADDUI    R1,R1,#-8  

ADD.D       F4,F0,F2    

stall            

BNE  R1,R2,Loop         ;delayed branch

S.D    F4,8(R1)     ;altered & interchanged with DADDUI

Execution time has been reduced from 10 clock cycles to 6.The stall after ADD.D is for the use by the S.D.

In the above example, we complete one loop iteration and store back one array element every 6 clock cycles, but the actual work of operating on the array element takes just 3 (the load, add, and store) of those 6 clock cycles. The remaining 3 clock cycles consist of loop overhead—the DADDUI and BNE—and a stall. To eliminate these 3 clock cycles we need

to get more operations within the loop relative to the number of overhead instructions.

A  simple  scheme  for  increasing  the  number  of  instructions  relative  to  the  branch

and overhead instructions is loop unrolling. Unrolling simply replicates the loop body multiple times, adjusting the loop termination code.

Loop unrolling can also be used to improve scheduling. Because it eliminates the branch, it allows instructions from different iterations to be scheduled together. In this case, we can eliminate the data use stall by creating additional independent instructions within the loop body. If we simply replicated the instructions when we unrolled the loop, the resulting use of the same registers could prevent us from effectively scheduling the loop. Thus, we will want to use different registers for each iteration, increasing the required register count.

In real programs we do not usually know the upper bound on the loop. Suppose it is n, and we would like to unroll the loop to make k copies of the body. Instead of a single unrolled loop, we generate a pair of consecutive loops. The first executes (n mod k) times and has a body that is the original loop. The second is the unrolled body surrounded by an outer loop that iterates (n/k) times. For large values of n, most of the execution time will be spent in the unrolled loop body.

2. Summary of the Loop Unrolling and Scheduling Example

To obtain the final unrolled code we had to make the following decisions and transformations:

Determine that it was legal to move the S.D after the DADDUI and BNE, and find the amount to adjust the S.D offset.

Determine  that unrolling  the  loop  would  be  useful  by  finding  that  the  loop iterations were independent, except for the loop maintenance code.

Use different registers to avoid unnecessary constraints that would be forced by using the same registers for different computations.

Eliminate the extra test and branch instructions and adjust the loop termination and iteration code.

Determine that the loads and stores in the unrolled loop can be interchanged by observing that the loads and stores from different iterations are independent. This transformation requires analyzing the memory addresses and finding that they do not refer to the same address. Unrolling is the growth in code size that results.